Viele Schülerinnen und Schüler tun sich gerade anfangs schwer mit der Polynomdivision. Dabei kannst du sie ganz einfach durchführen und anwenden, wenn du schriftlich dividieren kannst. In diesem Artikel zeigen wir dir, wie Polynomdivision funktioniert und wofür du sie einsetzen kannst.
So funktioniert die Polynomdivision
Einen guten ersten Überblick über die Polynomdivision gibt dir das folgende Video
[su_vimeo url=“https://vimeo.com/319805006″]
[su_box title=“Das Wichtigste in Kürze“ box_color=“#e35c37″ title_color=“#ffffff“]
Mit der Polynomdivision kannst du ein Polynom durch ein anderes Polynom teilen. Als Ergebnis erhältst du wieder ein Polynom. Du benötigst die Polynomdivision, um Nullstellen einer Funktion zu berechnen.
Die Polynomdivision funktioniert wie ganz ähnlich wie das schriftliche Dividieren. Du benötigst die folgenden 3 Schritte:
- Richtiges Aufschreiben
- Schritt für Schritt dividieren
- Rückmultiplizieren und Rest aufschreiben.
Im Beispiel sieht das wie folgt aus:
Eine Polynomdivision durchführen anhand eines Beispiels
Damit du dir einen ersten Überblick über die Polynomdivision verschaffen kannst, rechnen wir nun ein kurzes Beispiel durch. Dazu dient uns die Aufgabe:
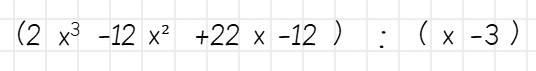
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=2]
[su_divider top=“no“ divider_color=“#eeeeee“]
Polynome dividierst du fast genauso wie Zahlen. Du schaust dir zunächst nur einen kleinen Teil des Dividenden an (das Polynom, das geteilt werden soll) und schaust, wie oft der Divisor (hier: x-3) hineinpasst. Hierzu musst du zunächst nur auf das jeweils erste Glied schauen, also auf 2x³ und x. Um zu wissen, wie oft x in 2x³ passt, teilst du 2x³ durch x und erhältst 2x² als Ergebnis. Das kannst du schon hinschreiben:
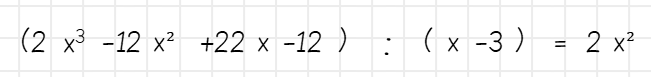
Nun beginnst du mit der Rückmultiplikation und multiplizierst 2x² mit x – 3. Das Ergebnis schreibst du unter den Dividenden ganz nach links.
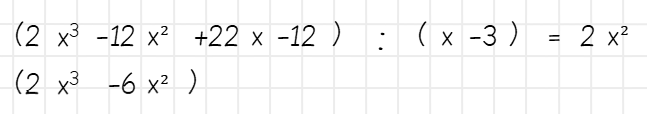
Nun bildest du die Differenz zwischen den ersten beiden Gliedern des Dividenden und dem Ergebnis der Rückmultiplikation und nimmst das nächste Glied dann nach unten – genau wie beim Dividieren von Zahlen.
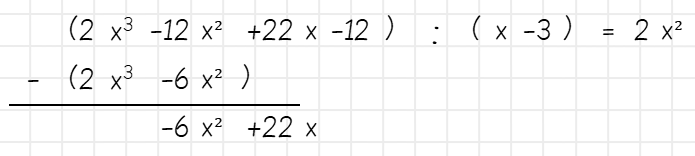
Diese Schritte setzt du nun fort, bis du als Differenz 0 erhältst.
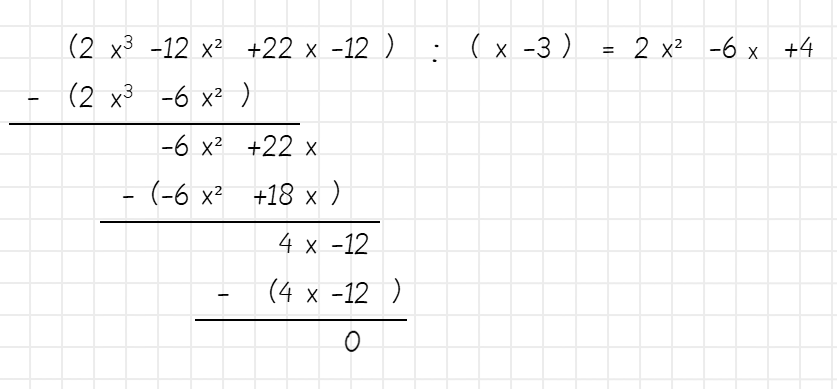
Und das ist auch schon alles!
Am Anfang ist es etwas ungewohnt, weil du nicht nur mit einer Zahl, sondern mit einem ganzen Polynom arbeitest und entsprechend mehrere einzelne Elemente rückmultiplizieren musst. Wenn du dich beim Teilen jedoch immer nur auf den jeweils ersten Wert konzentrierst und beim Rückmultiplizieren nichts vergisst, wird es mit etwas Übung ganz einfach.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=1]
[su_divider top=“no“ divider_color=“#eeeeee“]
Polynomdivision erklärt
Was ist ein Polynom?
Ein Polynom ist eine Summe von Vielfachen von Potenzen mit natürlichzahligen Exponenten einer Variable. Diese Definition hat vier Bestandteile, die du dir merken musst. Wir erklären sie im folgenden einzeln, damit du noch besser verstehst, was ein Polynom ist.
Bestandteil 1: Variable
Jedes Polynom hat mindestens eine Variable, also zum Beispiel x oder a und b (wie bei den binomischen Formeln – denn Binome sind Polynome mit zwei Summanden).
Bestandteil 2: Potenzen mit natürlichzahligen Exponenten
Die Variable oder Variablen kommen in Polynomen normalerweise als Potenzen mit unterschiedlichen Exponenten vor, also zum Beispiel x³ und x. Wenn der Exponent der Variable 0 ist, ergibt dies im Ergebnis 1, auch das ist möglich. In diesem Fall wird die Null nämlich zu den natürlichen Zahlen gerechnet, auch wenn dies nicht immer der Fall ist.
Bestandteil 3: Vielfache
Die einzelnen Potenzen der Variable können mit unterschiedlichen Faktoren vorkommen. Normalerweise bestehen Polynome nicht nur aus Potenzen, die mit dem Faktor 1 multipliziert werden, sondern mit allen möglichen Faktoren. Dies können auch Bruchzahlen oder Dezimalbrüche sein. Und da ein Vielfaches von x0 = 1 ebenfalls vorkommen kann, haben viele Polynome auch Konstanten. Außerdem können die Faktoren natürlich negativ sein.
Bestandteil 4: Summe
Die verschiedenen Vielfachen der Variablen werden aufsummiert, um ein Polynom zu erhalten. Dies sieht dann zum Beispiel so aus:
2x³ – 4x² + 12x + 9
Warum macht man überhaupt eine Polynomdivision?
Der Sinn der Polynomdivision ist in den meisten Fällen, Nullstellen einer Funktion zu finden bzw. eine Gleichung zu lösen. Du benötigst die Polynomdivision immer dann, wenn der höchste Exponent größer als 2 ist. Für quadratische Gleichungen und Funktionen kannst du einfach die pq-Formel oder die ABC-Formel anwenden, um die Nullstellen zu finden. Bei Gleichungen höheren Grads funktionieren diese Formeln jedoch nicht mehr.
Jedes Polynom lässt sich nämlich als Produkt aus sogenannten Linearfaktoren geschrieben werden, und zwar immer so viele, wie der Grad der Funktion ist (also der höchste vorkommende Exponent der Variable). Ein Linearfaktor ist die Differenz aus der Variable (zum Beispiel x) und einer Nullstelle. Das hört sich zunächst kompliziert an, ist aber eigentlich ganz einfach.
Ein Produkt wird immer dann 0, wenn (mindestens) einer der Faktoren gleich 0 ist, also.
3 • 2 • 0 = 0
oder
17 • 0 •12 • 394 = 0.
Sobald ein Faktor den Wert 0 hat, sind die anderen Faktoren egal – der ganze Ausdruck nimmt dann den Wert 0 an.
Das Polynom x³ – 7x² + 14x – 8 hat beispielsweise die Nullstellen 1, 2 und 3. Das bedeutet, wenn x die Werte 1, 2 oder 3 annimmt, nimmt das Polynom den Wert 0 an. Du kannst es daher auch anders schreiben, nämlich als (x – 1) • (x – 2) • (x – 3), denn wenn x = 1 ist, wird x – 1 = 0 – und damit der gesamte Ausdruck.
Wenn du nur eine Nullstelle eines Polynoms 3. Grades kennst, weißt du, dass ein Linearfaktor (x – Nullstelle) ist. Wenn du das Polynom nun durch diesen Ausdruck teilst, erhältst du das Produkt der beiden anderen Linearfaktoren. Dies ist quadratisch – denn du hast es durch ein lineares Polynom geteilt – und du kannst dieses dann mit den Methoden lösen, die du kennst.
Die Polynomdivision Schritt für Schritt
Oben hast du bereits anhand eines Beispiels die einzelnen Schritte der Polynomdivision kennengelernt. Hier stellen wir sie dir noch einmal einzeln vor. Dabei gehen wir die Aufgabe aus dem letzten Abschnitt durch: (x³ – 7x² + 14x – 8) : (x – 1).
Die Klammern sind hier wichtig, denn wegen der Regel Punkt- vor Strichrechnung würdest du sonst nur 8 durch x teilen.
Schritt 1: Richtig aufschreiben
Das hört sich banal an, aber wenn du die Polynome nicht richtig aufschreibst, kannst du sie nicht durcheinander teilen. Der Dividend (das Polynom, das geteilt werden soll) steht links, dahinter das Geteiltzeichen, und dann folgt der Divisor, also das Polynom, durch das du teilst. Auch hier gilt: an die Klammern denken!

Schritt 2: Variable durch Variable teilen
Viele sind von der Polynomdivision abgeschreckt, weil sie nicht wissen, wie sie erkennen sollen, wie oft ein Polynom wie x – 1 in ein anderes passt. Das musst du aber gar nicht. Bis zum letzten Schritt kannst du die -1 getrost vergessen und dich nur um die Variable kümmern. Du prüfst also lediglich, wie oft x in x³ passt. Das Ergebnis ist wieder ein Vielfaches einer Potenz von x, in diesem Fall x², denn x³ : x = x². Dies schreibst du rechts neben das Gleichheitszeichen.

Schritt 3: Rückmultiplikation
Die Rückmultiplikation kennst du vom schriftlichen Dividieren. Du musst nun das Ergebnis (x²) mit dem Divisor (x – 1) multiplizieren. Das Produkt aus beiden schreibst du unter den Dividenden, und zwar an die Stelle, an der du angefangen hast zu teilen – also direkt unter x³.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=3]
[su_divider top=“no“ divider_color=“#eeeeee“]
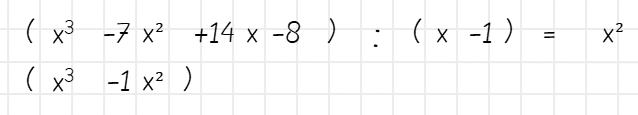
Schritt 4: Rest berechnen
Im nächsten Schritt ziehst du die Rückmultiplikation von den ersten Stellen des Dividenden ab – und zwar immer von so vielen Stellen wie die Rückmultiplikation auch hat. Dann nimmst du das nächste Glied des Divisors nach unten, um weiter dividieren zu können.
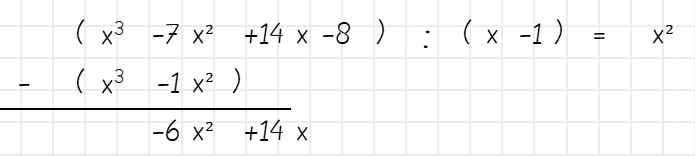
Und immer so weiter bis zum Schluss
Dieses Vorgehen wiederholst du so lange, bis du als Rest 0 unterm Strich stehen hast.
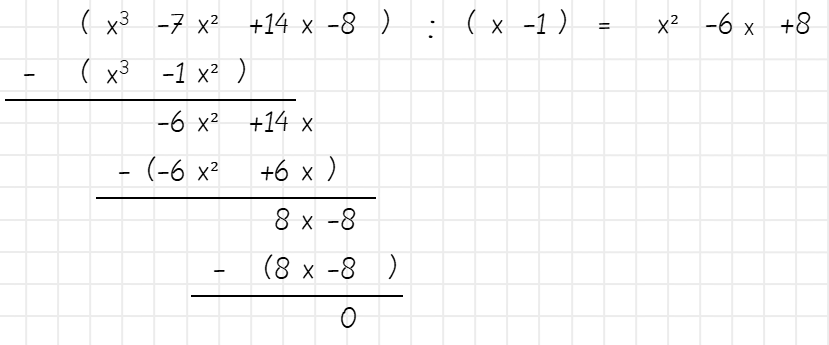
Damit hast du diese Aufgabe gelöst.
Polynomdivision mit Rest
Allerdings gehen natürlich nicht alle Polynomdivisionen ohne Rest auf. Wenn du einen Rest hast, bedeutet das, dass der Divisor kein Linearfaktor des Polynoms ist – du also möglicherweise mit einer falschen Nullstelle rechnest. Manchmal stellen deine Lehrer*innen dir jedoch bewusst Aufgaben, in denen ein Rest vorkommt.
In diesem Fall schreibst du rechts neben das Ergebnis „Rest: “ und dahinter den verbleibenden Rest hin. Woher weißt du aber, wann du mit der Polynmdivision aufhören sollst? Ganz einfach, das Ergebnis sollte keine negativen Exponenten enthalten. Bevor dies also der Fall ist, hörst du auf und schreibst den Rest einfach neben das Ergebnis.
Im folgenden Beispiel bleibt ein Rest übrig, den man einfach neben das Ergebnis schreibt.

3 Beispielaufgaben mit Lösungen zur Polynomdivision
Hier findest du noch weitere Anwendungsaufgaben für die Polynomdivision.
[su_box title=“Aufgabe 1:“ box_color=“#6eb5c5″ title_color=“000000″](x³ – 4x² – 77x + 360) : (x + 9)[/su_box]
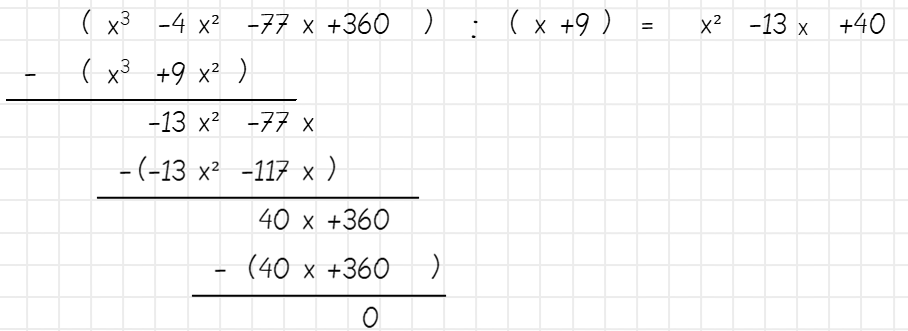
[su_box title=“Aufgabe 2:“ box_color=“#6eb5c5″ title_color=“000000″](3x³ + 30x² + 93x + 90) : (x + 3)[/su_box]

[su_box title=“Aufgabe 3:“ box_color=“#6eb5c5″ title_color=“000000″](2x³ – 3x² – 19x + 48) : (x + 3)[/su_box]
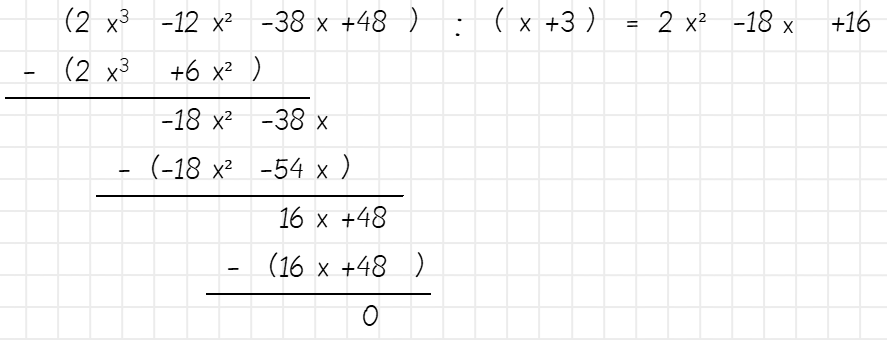
[su_box title=“Tipp! Mach dich jetzt fit für die Klausur mit unseren Arbeitsheften:“ box_color=“#006c84″ title_color=“#ffffff“]
[/su_box]Die wichtigsten Fragen zur Polynomdivision beantwortet
Wir haben noch nicht alle deine Fragen beantwortet? Dann schau am besten in diesen FAQ zur Polynomdivision nach, schicke uns eine E-Mail oder hinterlasse einen Kommentar.
[su_accordion]
[su_spoiler title=“Welche anderen Verfahren zur Linearfaktorzerlegung gibt es, die ich statt der Polynomdivision anwenden kann?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Für Polynome zweiten Grades kannst du die pq-Formel und die ABC-Formel anwenden. Für Polynome 3. Grades gibt es außer der Polynomdivision noch das Horner-Schema, das zum selben Ergebnis führt.
Antwort[/su_spoiler]
[su_spoiler title=“Wie kann ich die erste Nullstelle finden?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Nullstellen eines Polynoms sind immer Teiler des freien Glieds, also der Konstante, die kein x mehr hat. Sie können positive oder negative Vorzeichen haben. Um die erste Nullstelle zu finden, bestimmst du also die Teiler der Konstante und probierst diese dann durch Einsetzen in das Polynom aus. Sobald du das erste Mal Null als Ergebnis erhältst, kannst du mit der Suche aufhören.
Antwort[/su_spoiler]
[su_spoiler title=“Was ist der Unterschied zwischen Polynomdivision und Horner-Schema?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Das Horner-Schema ist ein Umformungsverfahren. Es nutzt grundsätzlich dieselben Voraussetzungen wie die Polynomdivision, macht diese jedoch (für manche) ein wenig leichter.[/su_spoiler]
[su_spoiler title=“Was mache ich falsch, wenn die Polynomdivision nicht funktioniert?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
„Nicht funktionieren“ heißt normalerweise, dass ein Rest bleibt. Prüfe daher noch einmal von Anfang an, ob du die Schritte, wie sie oben beschrieben sind, alle richtig durchgeführt hast. Bleibt immer noch ein Rest, so machst du nichst falsch. Du kannst den Rest dann einfach neben das Ergebnis schreiben.[/su_spoiler]
[su_spoiler title=“Wie mache ich die Probe zur Polynomdivision?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Du kannst das Ergebnis einfach mit dem Divisor multiplizieren und musst als Ergebnis wieder den Dividenden erhalten – dann hast du alles richtig gemacht.[/su_spoiler]
[su_spoiler title=“Kann ich auch eine Polynomdivision mit mehreren Variablen durchführen?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Ja, das geht auch. Du gehst dabei genauso vor wie oben beschrieben, an der Vorgehensweise ändert sich nichts.[/su_spoiler]
[/su_accordion]
Zusammenfassung
[featured_snippet image=“https://nachgeholfen.de/wp-content/uploads/2019/02/img_5c745b95ad6c1-e1551129513761.png“ image_alt=“Beispiel Polynomdivision“]
Mit Hilfe der Polynomdivision kannst du Nullstellen von Funktionen ermitteln und eine Linearfaktorzerlegung vornehmen. Du gehst in vier Schritten vor:
- Aufgabe richtig aufschreiben
- Variable durch Variable teilen und Ergebnis notieren
- Rückmultiplikation Ergebnis • Divisor
- Differenz bilden und Rest ermitteln
Diese Schritte gehst du immer wieder durch, bis du nicht weiter teilen kannst. Teilst du durch einen Linearfaktor des Polynoms, so bleibt kein Rest übrig.
[/featured_snippet]
Mehr Unterstützung und Training zu diesem Thema findest du in unseren Arbeitsheften. Wenn du eine persönliche Betreuung suchst, kann dir unsere Online-Nachhilfe nützlich sein!
[su_box title=“Tipp! Mach dich jetzt fit für die Klausur mit unseren Arbeitsheften:“ box_color=“#006c84″ title_color=“#ffffff“]
[/su_box]

