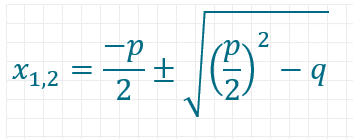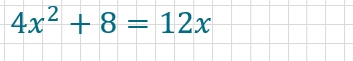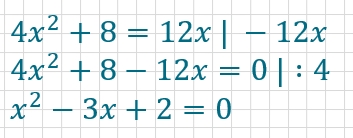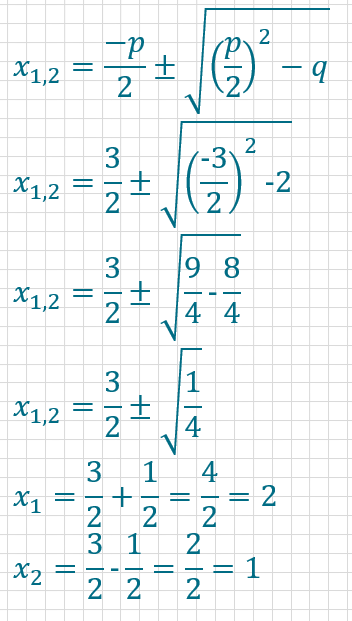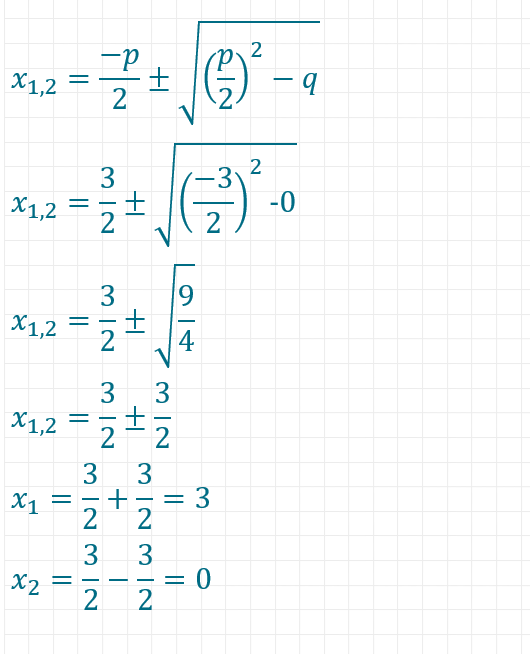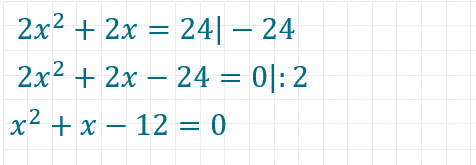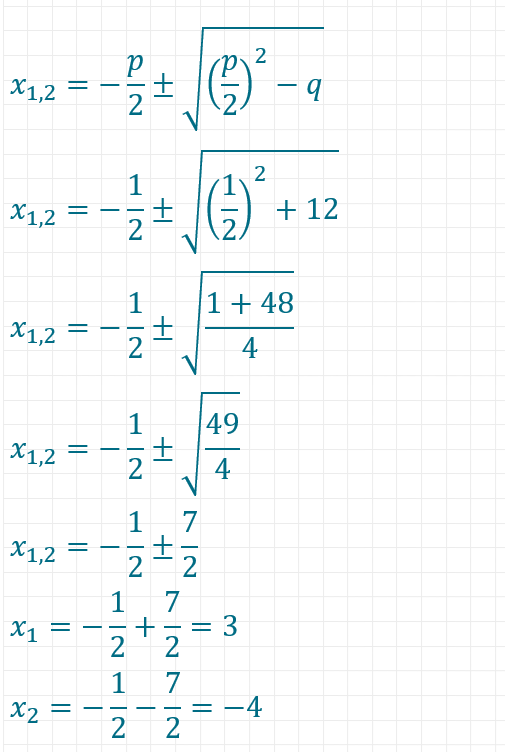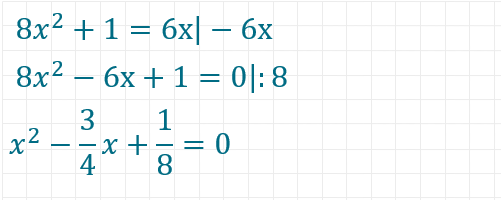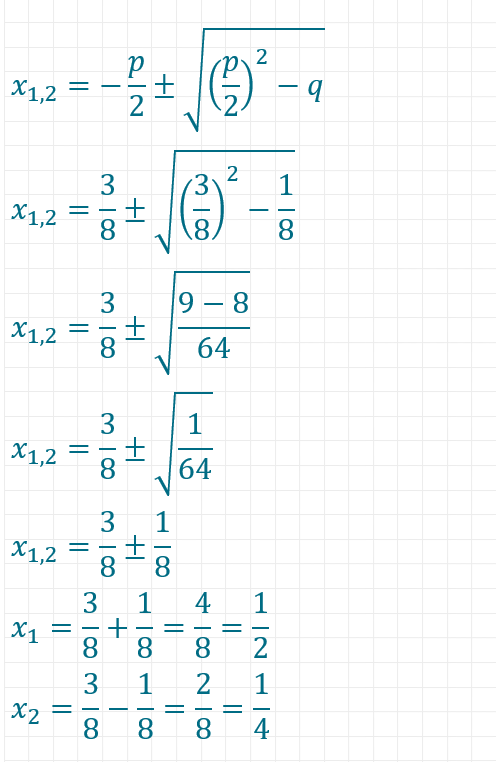Mit der pq-Formel kannst du ganz einfach quadratische Gleichungen lösen. Umformen – einsetzen – und schon hast du das Ergebnis. Wir zeigen dir in diesem Artikel alles, was du zu diesem Thema wissen musst.
So löst du quadratische Gleichungen mit der pq-Formel
Schau dir am besten zunächst unser Video zur pq-Formel an, um einen guten Einstieg ins Thema zu bekommen.
Quadratische Gleichungen haben die (Normal-)Form:
Wenn die Gleichung in dieser Form vorliegt, kannst du allein aus p und q errechnen, welche Werte x annehmen darf, damit die Gleichung gelöst wird. Dafür setzt du p und q in die pq-Formel ein:
Du erhältst meistens zwei mögliche Ergebnisse für x. Es ist jedoch auch möglich, dass es nur eine oder gar keine Lösung für die quadratische Gleichung gibt. Wie du eine Gleichung in die Normalform bringst, wie du die pq-Formel anwendest und sie ausrechnest, zeigen wir dir im Folgenden.
Quadratische Gleichungen lösen mit der pq-Formel – im Beispiel
Eine typische Aufgabe zur pq-Formel besteht darin, die Lösung für eine quadratische Gleichung zu finden. Ein ganz einfaches Beispiel ist das folgende, in dem wir die Aufgabe für dich bereits gelöst haben. Eine genauere Erklärung der einzelnen Schritte folgt anschließend.
Zunächst bringst du die Gleichung durch Umformen in Normalform.
Dann setzt du die Werte für p und q in die pq-Formel ein und erhältst die Lösung.
Das ging dir noch zu schnell? Kein Problem. Denn wir erklären die pq-Formel nun Schritt für Schritt.
[quads id=1]Die pq-Formel erklärt
Mit der pq-Formel kannst du jede quadratische Gleichung mit einer Variablen lösen – sofern es überhaupt eine Lösung für die Gleichung gibt.
Quadratische Gleichungen können in der folgenden Form geschrieben werden:
x2 + ax + b = 0
Das bedeutet nicht, dass jede quadratische Gleichung, die du lösen sollst, genau diese Form bereits besitzt. Oft musst du die Gleichung umformen, damit sie diese Form – die Normalform – erhält. Die Normalform zeichnet sich durch zwei Eigenschaften aus:
- Auf der rechten Seite der Gleichung steht 0 und nichts anderes. Alle anderen Bestandteile stehen auf der linken Seite.
(Hinweis: Links und rechts können auch vertauscht werden. Wichtig ist, dass auf der einen Seite vom Gleichheitszeichen 0 steht und er Rest auf der anderen Seite. Üblich ist, dass die 0 rechts vom Gleichheitszeichen steht.) - x2 hat keinen Koeffizienten.
Wenn du die Normalform durch Umformen erreicht hast, kannst du ganz leicht die pq-Formel anwenden.
Eine quadratische Gleichung hat entweder keine, eine oder zwei Lösungen. Anders als zum Beispiel bei linearen Gleichungen kann es nämlich mehr als ein x geben, für das die Gleichung zutrifft. Dies liegt an der Quadrierung von x und daran, dass x2 für x und -x dasselbe Ergebnis hat.
Wie lautet die pq-Formel?
DIe pq-Formel haben wir weiter oben bereits eingeführt. Hier ist sie noch einmal:
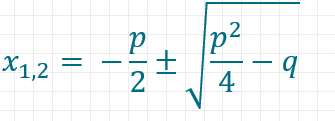
Die schlechte Nachricht hierzu lautet, dass du sie auswendig lernen musst. Daran führt leider kein Weg vorbei, wenn du in der Klassenarbeit mit ihr quadratische Gleichungen lösen möchtest. Die gute Nachricht: Das geht relativ schnell, vor allem, wenn du sie häufig anwendest. Tipps, wie du dir die pq-Formel leichter merken kannst, folgen weiter unten im Artikel.
Was bedeuten die einzelnen Bestandteile der Formel?
Wie bereits beschrieben kann eine quadratische Gleichung bis zu zwei verschiedene Lösungen haben. Mit der pq-Formel erhältst du beide, daher beginnt sie mit x1,2. Das erste mögliche x erhältst du, wenn du die Formel mit + ausrechnest, das zweite durch die Anwendung von -. (Die Mitternachts- bzw. ABC-Formel, die eine Alternative zur pq-Formel darstellt, funktioniert übrigens nach demselben Prinzip.)
Nun musst du natürlich noch wissen, was p und q sind. Wir haben oben geschrieben, dass eine quadratische Gleichung immer auf die Form
x2 + ax + b = 0
gebracht werden kann. Wenn du a nun durch p und b durch q ersetzt, hast du alle Elemente der Formel gefunden. Nun kann es an die Anwendung gehen.
[quads id=2]Wie wende ich die pq-Formel an?
Du wendest die pq-Formel ganz einfach in nur zwei Schritten an.
Schritt 1: Du formst deine Gleichung um, damit sie die Form x² + ax + b = 0 (bzw. x² + px + q = 0) hat. Dies ist erforderlich, damit du weißt, welche Werte p und q annehmen.
Schritt 2: Du setzt p und q in die pq-Formel ein und rechnest die Ergebnisse aus.
Das Ganze ist wirklich sehr einfach, weil du es mit etwas Übung immer wieder in der gleichen Form anwenden kannst. Selbst, wenn du die Formel nicht verstehst, kannst du sie einfach nach dem folgenden Muster auflösen. Wir zeigen dir das anhand von 3 Rechenbeispielen.
3 Beispielaufgaben mit Lösungen zur pq-Formel
Schritt 1: Umformung auf Normalform
Gleichungen kannst du umformen, indem du immer für beide Seiten (links und rechts vom Gleichheitszeichen) dieselbe Rechenoperation durchführst. Um die Normalform zu erhalten, bringst du zunächst alle Elemente auf die linke Seite. Dann fasst du die einzelnen Elemente anhand des Exponenten von x zusammen, also alle x2, alle x und alle Konstanten. Zum Schluss teilst du die gesamte Gleichung durch den Faktor von x2.
Im Beispiel sieht das so aus:
1. Alle Elemente auf die linke Seite bringen
2. Elemente nach den Exponenten von x zusammenfassen
3. Durch den Faktor von x teilen
[quads id=3]Schritt 2: Anwendung der Formel
Nachdem du nun Normalform ermittelt hast, kannst du p und q ganz einfach ablesen. Wichtig: Die Vorzeichen gehören ebenfalls zu p und q, also p = -3 und q = 0.
Nun setzt du p und q in die pq-Formel ein und erhältst das folgende Ergebnis. Denke daran, dass Minus mal Minus Plus ergibt, wenn du p oder q mit negativem Vorzeichen einsetzt!
Als mögliche Lösungen für die Gleichung hast du also 3 und 0 identifiziert. Wir können nun diese beiden Werte in die ursprüngliche Gleichung einsetzen, um sie zu überprüfen.
Überprüfung für x1= 3:
4 • 32 – 6 • 3 + 9 = 2 • 32 + 9
⇔ 4 • 9 – 18 + 9 = 2 • 9 + 9
⇔ 36 – 18 + 9 = 18 + 9
⇔ 27 = 27
Das erste Ergebnis stimmt also schon einmal.
Überprüfung für x2= 0:
4 • 02 – 6 • 0 + 9 = 2 • 02 + 9
⇔ 0 – 0 + 9 = 0 + 9
⇔ 9 = 9
Auch das zweite Ergebnis stimmt, wir haben also die pq-Formel richtig angewendet.
Manchmal kommt es vor, dass der Wert, der unter der Wurzel steht, kleiner als 0 ist. In diesem Fall kannst du natürlich keine Quadratwurzel ziehen. Die quadratische Gleichung hat dann keine Lösung. Ist der Wert unter der Wurzel genau gleich 0, so hat die Gleichung nur eine Lösung.
Schritt 1: Umformung auf Normalform
Schritt 2: Anwendung der Formel
Schritt 1: Umformung auf Normalform
Schritt 2: Anwendung der Formel
Mehr Aufgaben und Lösungen findest du in unsren Arbeitsheften, mit denen du die pq-Formel perfekt üben kannst.
Wie kannst du dir die pq-Formel am besten merken?
Wie bereits gesagt führt leider kein Weg daran vorbei, die pq-Formel auswendig zu lernen. Aber wenn du sie dir genauer anschaust und in ihre Bestandteile zerlegst, fällt es dir sicher ein wenig leichter.
- q kannst du dir am einfachsten merken. Du musst es nur abziehen und (zunächst) nichts weiter damit machen. Der Teil der Formel, der q betrifft, ist also nichts besonderes – das passt dazu, dass q in der quadratischen Gleichung für die Zahl steht, die als einzige kein x hat. Du musst dir hier nur das Minuszeichen vor dem q merken!
- p halbierst du, und zwar einmal vor und einmal nach dem Plusminus-Zeichen. Du kannst dir als Eselsbrücke merken, dass du je ein halbes p pro Lösung für x brauchst. deswegen teilst du auch das p (auch wenn das mathematisch natürlich so nicht korrekt ist). Und einmal kommt der Ausdruck mit – und dann mit + vor.
- Das zweite p/2 quadrierst du – dann ziehst du aber auch gleich wieder die Wurzel. Da es ja Unsinn wäre, etwas zu quadrieren und daraus wieder die Wurzel zu ziehen, packst du das q mit unter das Wurzelzeichen. Eine Qurzel sozusagen.
Wenn du dir die einzelnen Elemente der pq-Formel vor Augen führst und dir für jedes einzelne überlegst, wie du es dir merken und in einen Zusammenhang bringen kannst, wirst du dir die Formel schnell einprägen können.
Die wichtigsten Fragen zur pq-Formel beantwortet
Du hast noch Fragen zur pq-Formel? Wir haben für dich die Antworten auf die wichtigsten Fragen zu diesem Thema zusammengestellt. Solltest du etwas nicht finden, kannst du uns gerne einen Kommentar schreiben.
Wann kannst du die pq-Formel einsetzen?
Die pq-Formel setzt du ein, um quadratische Gleichungen zu lösen oder um Nullstellen in quadratischen Funktionen zu bestimmen. Ob du die Formel anwenden kannst, siehst du daran, ob die Gleichung bzw. die Funktion eine Gleichung 2. Grades ist. Das bedeutet, der höchste Exponent, der bei x vorkommt, muss die 2 sein. Suche also nach x² in der Gleichung. Wenn du eins findest und kein x mit höherem Exponenten vorkommt, kannst du die pq-Formel sehr wahrscheinlich einsetzen.
Ist die pq-Formel das gleiche wie die Mitternachtsformel?
Nein. Die pq-Formel und die Mitternachtsformel (oder ABC-Formel) dienen beide dazu, quadratische Gleichungen zu lösen. Sie liefern dieselben Ergebnisse, sind jedoch in der Anwendung und natürlich auch in der Form leicht unterschiedlich.
Tipp: Mehr über die ABC-Formel / Mitternachtsformel kannst du in unserem Artikel zum Thema nachlesen.
Wann verwendest du die pq-Formel und wann die Mitternachtsformel / ABC-Formel?
Das hängt zunächst einmal natürlich von der Aufgabenstellung ab. Wenn ihr in der Schule gerade die pq-Formel bearbeitet habt, sollst du wahrscheinlich zeigen, dass du sie beherrschst – und sie entsprechend anwenden. Dasselbe gilt natürlich auch für die Mitternachtsformel.
Ansonsten gilt: Für die pq-Formel musst du die quadratische Gleichung in Normalform bringen, für die Mitternachtsformel reicht es, alle Summanden auf eine Seite zu bringen, sodass rechts vom Gleichheitszeichen nur noch die 0 steht. Wenn du beide Formeln auswendig kannst und die Wahl hast, kannst du dir mit der Mitternachtsformel so einen Rechenschritt bei der Umformung sparen.
Wahrscheinlich wirst du dir eine der beiden Formeln etwas besser merken können als die andere. Wenn du in der Klassenarbeit dann aussuchen darfst, mit welcher Formel du die Aufgabe löst, nimm am besten immer die, bei der du dich sicherer fühlst.
Wie hängen die pq-Formel und die Mitternachtsformel miteinander zusammen?
Du kannst die ABC-Formel ganz leicht aus der pq-Formel ableiten, denn beide liefern Lösungen für quadratische Gleichungen. Der Unterschied ist nur, dass du bei der Vorbereitung der Gleichung für die pq-Formel einen Schritt mehr gehen musst.
Um die Mitternachtsformel anwenden zu können, benötigst du die quadratische Gleichung in der folgenden Form:
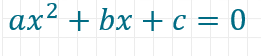
Da x2 in der pq-Formel keinen Exponenten haben darf, teilst du die gesamte Gleichung durch a, um p und q zu erhalten, also:
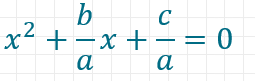
Du weißt nun, dass
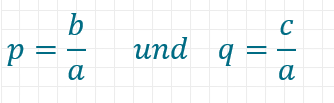
ist. Dies kannst du in die pq-Formel einsetzen. Du erhältst dann:
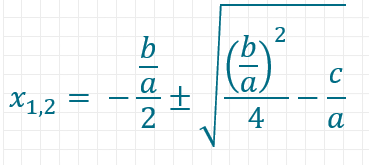
Durch Umformen der Gleichung erhältst du die ABC-Formel:
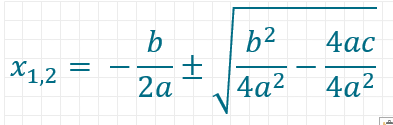
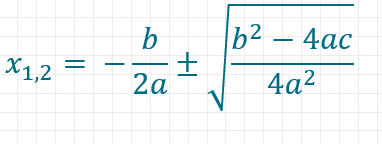
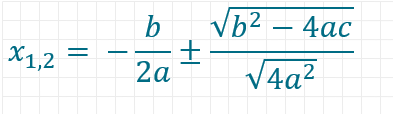

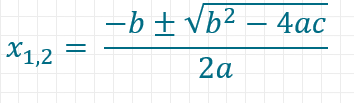
Wann liefert die pq-Formel zwei Ergebnisse, wann eins und wann kein Ergebnis?
Im Normalfall sollte die pq-Formel zwei Ergebnisse liefern. Die meisten Aufgaben, die du in der Schule lösen sollst, sind bewusst so aufgebaut, dass du zwei Lösungen erhältst.
Dennoch kommt es vor, dass es nur eine oder sogar gar keine Lösung gibt. Nur eine Lösung erhältst du immer dann, wenn der Wert unter dem Wurzelzeichen gleich Null ist. Denn irgendetwas plus Null ist dasselbe wie irgendetwas minus Null – beide Rechenwege der pq-Formel führen also zum selben Ergebnis.
Ist der Wert unter dem Wurzelzeichen negativ, so kannst du keine Wurzel ziehen. Man könnte hier mit komplexen Zahlen arbeiten. Das wird während der Schulzeit aber wohl niemand von dir verlangen. Du kannst also als Lösung hinschreiben, dass das Ergebnis nicht definiert ist.
Was kannst du tun, wenn die pq-Formel nicht funktioniert?
Wie in der letzten Frage beschrieben funktioniert die pq-Formel immer dann (und nur dann!) nicht, wenn unter dem Wurzelzeichen ein negativer Wert steht. Ist dies der Fall, solltest du als erstes noch einmal deinen Rechenweg überprüfen. Es passiert gerade beim Umformen der Gleichung in die Normalform und beim Einsetzen von p und q in die Formel leicht, dass man mal ein Vorzeichen vertauscht – und schon stimmt gar nichts mehr. Wenn du also deine Lösung noch einmal prüfst, achte dabei vor allem auf die Vorzeichen. Es ist wahrscheinlicher, dass du hier einen Flüchtigkeitsfehler gemacht hast als dass dein*e Lehrer*in dir tatsächlich eine unlösbare Aufgabe gibt.
Bist du dir sicher, dass dein Rechenweg stimmt, rechnest du zunächst so weit, wie du kommst. Das heißt, du formst die Gleichung um, setzt p und q in die Formel ein und rechnest den Wert unter der Formel aus. Zum Schluss schreibst du als Antwort hin, dass das Ergebnis der Aufgabe nicht definiert ist.
Wie funktioniert die pq-Formel ohne p bzw. ohne q?
Ohne p und ohne q funktioniert die pq-Formel natürlich nicht, und tatsächlich hat jede quadratische Gleichung ein p und ein q – auch wenn du es vielleicht nicht sofort erkennst.
In der Form x2 = 0 scheinen p und q zu fehlen, aber das bedeutet einfach, dass sowohl p als auch q gleich Null sind. Die Lösung der pq-Formel ist in diesem Fall auch besonders einfach – du kannst es ja einmal ausprobieren.
Sieht deine quadratische Gleichung so aus: x2 + x + 1 = 0, fragst du dich vielleicht auch, welchen Wert p annimmt. Da kein explizites p vor dem x steht, bedeutet dies, dass x mit 1 multipliziert wird. p ist also in diesem Fall gleich mit 1.
Wenn es also gar keine Konstante gibt, ist q gleich mit 0. Gibt es kein x (ohne Quadrat), so ist p gleich 0. Fehlt vor dem x der Koeffizient, dann ist p gleich 1.
Kann man die pq-Formel auch in Ungleichungen anwenden?
Ja, du kannst die pq-Formel auf jeden Fall in Ungleichungen anwenden. Du gehst die Schritte genauso durch wie bei Gleichungen und bringst die Ungleichung erst einmal in Normalform.
Achtung: Bei Ungleichungen musst du darauf achten, dass sich das Größer- bzw. Kleinerzeichen umdreht, wenn du mit einer negativen Zahl multiplizierst oder durch eine negative Zahl dividierst!
Hast du die Ungleichung in Normalform vorliegen, setzt du p und q einfach in die pq-Formel ein – also alles wie gehabt. Allerdings ersetzt du das Gleichheitszeichen in der Formel durch das entsprechende Zeichen aus der Normalform der quadratischen Gleichung. Wenn dort zum Beispiel < steht, setzt du dieses Zeichen auch in die pq-Formel ein und erhältst so deine Lösung. Das Ergebnis sind dann keine Werte, sondern Lösungsbereiche, zum Beispiel x1 > 2, x2 > -1.
Die Interpretation des Ergebnisses ist jedoch ein wenig anders, denn beide Lösungen müssen zutreffen, damit die Gleichung wirklich größer 0 ist.
Kann man die pq-Formel auch bei Gleichungen 3. Grades (x³) anwenden?
Die pq-Formel ist nur für Gleichungen zweiten Grades gültig. Trotzdem kannst du bei der Lösung von Gleichungen 3. Grades die pq-Formel anwenden. Allerdings musst du die Gleichung erst einmal in zwei Komponenten zerlegen: eine Gleichung ersten und eine Gleichung zweiten Grades, die du miteinander multiplizierst.
Dafür musst du eine mögliche Lösung der Gleichung bereits kennen. Diese findest du durch Ausprobieren (ja, wirklich!) oder dein*e Lehrer*in gibt dir die Lösung vor. Ist eine mögliche Lösung zum Beispiel x = 3, so weißt du, dass du deine Gleichung schreiben kannst als Produkt aus einer Gleichung zweiten Grades und (x – 3), denn wenn x = 3 ist, ist x – 3 = 0 und damit ist das gesamte Produkt (und die Gleichung) auch gleich 0.
Mit Hilfe der Polynomdivision kannst du nun deine Gleichung 3. Grades durch x – 3 teilen und erhältst dann eine Gleichung zweiten Grades. Diese kannst du mit der pq-Formel lösen. Die beiden Lösungen, die du dann erhältst, plus die erste bereits gefundene Lösung sind die drei Lösungen der Gleichung 3. Grades.
Wie nutzt man die pq-Formel bei negativen Exponenten?
Negative Exponenten bedeuten, dass x (dann mit positivem Exponenten) im Nenner eines Bruchs steht. Die pq-Formel funktioniert allerdings nur bei positiven Exponenten. Daher musst du die Gleichung erst einmal so umformen, dass du die negativen Exponenten loswirst.
Am einfachsten kannst du dies anhand eines Beispiels verstehen. Nimm die Funktion
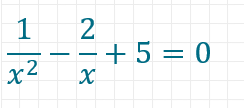
Als erstes ist wichtig, festzustellen, dass diese Funktion für x = 0 nicht definiert ist, weil die Division durch 0 nicht definiert ist. Dies solltest du in der Lösung einer solchen Aufgabe auf jeden Fall erwähnen. Dann kannst du die Gleichung umformen, indem du mit x2 multiplizierst. Du erhältst dann:
1 – 2x + 5x2 = 0
Diese Gleichung kannst du nun mit der pq-Formel ganz normal lösen.
Wie kannst du mit der pq-Formel Nullstellen berechnen?
Eine quadratische Funktion hat die Form f(x) = ax2 + bx + c = 0. Wenn du die Nullstellen dieser Funktion berechnen sollst, sucht du die Punkte, an denen f(x) = 0 ist. Und das ist der Fall, wenn ax2 + bx + c = 0 ist. Du setzt also einfach die Funktionsgleichung gleich Null, formst diese dann in die Normalform um und löst anschließend mit der pq-Formel wie oben beschrieben die Aufgabe.[/su_spoiler]
Kann man die pq-Formel auch für Gleichungen mit zwei Variablen anwenden?
Gleichungen mit zwei oder mehreren Variablen kannst du nicht mit der pq-Formel lösen. Wenn neben x noch eine weitere Variable in einer quadratischen Gleichung vorkommt, kannst du sie lediglich als Variable stehen lassen und sie in die pq-Formel einsetzen.
Auch dies versteht man leichter mit einem Beispieil.
x2 +2x – 2z = 0
z ist eine weitere Variable. Da die quadratische Gleichung bereits in der Normalform vorliegt, kannst du die pq-Formel aufstellen.
-1 ± √(1 + 2z)
Weiter kannst du die Gleichung nicht lösen. Allerdings solltest du noch angeben, welche Werte z annehmen darf, damit die Gleichung lösbar ist. Denn – wie du weiter oben nachlesen kannst – darf der Wert unter dem Wurzelzeichen nicht negativ werden. Du kannst nämlich keine Wurzel einer negativen Zahl ziehen. Um den Definitionsbereich von z zu ermitteln, stellst du daher die folgende Ungleichung auf:
1 + 2z ≥ 0
Dies kannst du umformen zu
z ≥ -0,5
Damit hast du die Aufgabe so weit gelöst, wie es möglich ist.
Zusammenfassung
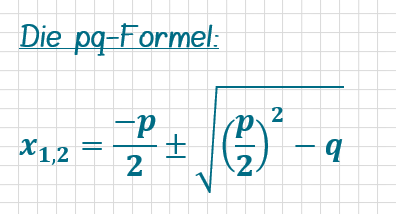
Mit der pq-Formel quadratische Gleichungen lösen:
- Gleichung in Normalform x2 + px + q = 0 bringen.
- p und q in die Formel einsetzen.
- Lösungen für x1 und x2 ausrechnen.
Ist der Wert unter der Wurzel negativ, so gibt es keine Lösung, ist er gleich Null, so gibt es nur eine Lösung.
Du brauchst noch Hilfe zur pq-Formel oder möchtest mehr üben? In unseren Arbeitsheften findest du jede Menge Aufgaben mit Lösungen zur pq-Formel. Individuelle Betreuung erhältst du in unserer Online-Nachhilfe!