In diesem Artikel erfährst du alles, was du wissen musst, um Nullstellen von Funktionen zu berechnen.
Was sind Nullstellen?
Nullstellen in Funktionen sind die Stellen, an denen der Graph der Funktion die x-Achse schneidet. Für die Nullstellen gilt also f(x) = 0 bzw. y(x) = 0.
Nicht jede Funktion hat zwangsläufig eine oder mehrere Nullstellen. Eine Gerade, die parallel zur x-Achse verläuft, schneidet diese beispielsweise nicht und hat daher auch keine Nullstellen. Genauso hat eine quadratische Funktion, die ober- oder unterhalb der x-Achse verläuft, keine Nullstelle.
Die maximale Anzahl der Nullstellen einer Funktion kannst du übrigens leicht ablesen: Sie entspricht dem Grad der Funktion, also dem höchsten Exponenten von x. Einzige Ausnahme: Die Funktion y = 0, die unendlich viele Nullstellen besitzt, da sie der x-Achse entspricht.
[quads id=1]Wozu muss man Nullstellen berechnen?
Nullstellen berechnest du, um etwas über den Verlauf des Graphen einer Funktion sagen zu können. So kannst du leichter eine Skizze anfertigen und hast schon erste Informationen über den Verlauf der Kurve.
Entsprechend zählt das Berechnen von Nullstellen zu den Grundlagen der Kurvendiskussion. Häufig musst du bereits Nullstellen berechnen, noch bevor du beispielsweise Ableitungen für die Funktionen ermittelst.
Je niedriger der Grad der Funktion, desto einfacher ist es, die Nullstellen zu berechnen. Du wendest auch unterschiedliche Methoden für verschiedene Arten von Funktionen an. Daher erklären wir dir im Folgenden, wie du für Funktionen unterschiedlichen Grads die Nullstellen berechnen kannst.
Nullstellen berechnen für verschiedene Arten von Funktionen
Lineare Funktionen
Lineare Funktionen haben maximal eine Nullstelle. Diese kannst du ganz einfach berechnen, indem du für y bzw. für f(x) 0 einsetzt und dann nach x auflöst.
Beispiel:
Berechne die Nullstelle für die Gleichung y = 5x + 7
Hierzu setzt du zunächst für y 0 ein:
0 = 5x + 7
Nun löst du nach x auf.
⇔ 0 = 5x + 7 | – 5x
⇔ -5x = 7 | : (-5)
⇔ x = -7/5 | – 5x
Die Nullstelle für diese Funktion liegt also bei x =-7/5.
Tipp: In diesem Artikel findest du noch mehr Informationen zu linearen Funktionen.
[quads id=2]Quadratische Funktionen
Nullstellen für quadratische Funktionen errechnest du mit der pq-Formel oder mit der Mitternachtsformel / ABC-Formel. Diese lautet:
Tipp: Eine ausführliche Erklärung zur pq-Formel findest du hier.
Um die pq-Formel anwenden zu können, bringst du deine Funktion zunächst in die Normalform y = x2 + px + q. p und q setzt du dann in die pq-Formel ein und erhältst als Ergebnis die Nullstellen der Funktion.
Beispiel:
Berechne die Nullstellen für die Funktion y = x2 + 2x – 3
Aus der Funktion kannst du ablesen, dass p = 2 und q = -3 ist. Diese Werte setzt du in die pq-Formel ein.
Die beiden Nullstellen der Funktion liegen also bei 1 und -3.
[quads id=3]Funktionen dritten und höheren Grades
Die Berechnung von Nullstellen mit einem x-Exponenten von 3 oder höher gestaltet sich schwieriger. Eine mögliche Methode, hier die Nullstellen zu berechnen, ist die Polynomdivision.
In diesem Video ist die Polynomdivision erklärt:
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
Ein Polynom hat die Form a0x0 + a1x1 + a3x2 + a3x3 + … . Konkret ist zum Beispiel x3 + 2x2 + x – 3 ein Polynom. Wenn du eine Funktion hast, steht links vom Gleichheitszeichen meist y oder f(x) und rechts steht ein Polynom.
Ein Polynom kannst du immer als Produkt aus n Polynomen mit der Potenz 1 darstellen, wobei n die höchste Potenz des Polynoms ist. Diese Faktoren, die als Produkt das Polynom ergeben, nennt man Linearfaktoren. Das Ziel der Polynomdivision ist es, das Polynom in seine Linearfaktoren zu zerlegen. Denn wenn ein Faktor eines Produkts 0 ist, ist auch das ganze Produkt gleich 0. Du musst daher dann nur noch die Nullstellen der einzelnen Linearfaktoren bestimmen. Da diese linear sind, ist das sehr einfach.
Im ersten Schritt musst du zunächst eine Nullstelle durch Probieren herausfinden. Oft bekommst du sie auch von deinem Lehrer oder deiner Lehrerin.
Beispiel
Gegeben sei die Funktion y = x3 + 5x2 + 2x – 8. Eine Nullstelle liegt bei x = 1. Bestimme die anderen beiden Nullstellen der Funktion
Schritt 1: Polynomdivision
Da die erste Nullstelle bei 1 liegt, ist der erste Linearfaktor des Polynoms (x – 1), denn hierfür liegt die Nullstelle ebenfalls bei 1. Nun musst du das Polynom x3 + 5x2 + 2x – 8 durch (x – 1) dividieren, um eine quadratische Funktion zu erhalten, die du dann mit der pq-Formel weiter lösen kannst.
Die Polynomdivision funktioniert wie das schriftliche Dividieren, das du bereits in der Grundschule gelernt hast. Für das Beispiel sieht die Polynomdivision wie folgt aus:
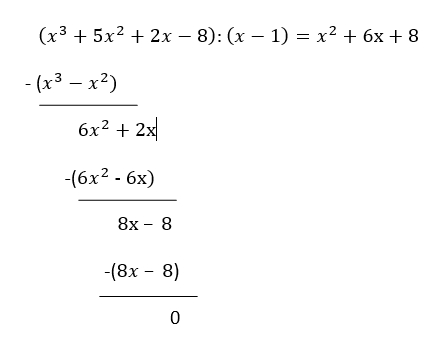Als Ergebnis erhältst du das Polynom x2 + 6x + 8. p ist also 6, q ist gleich 8. In die pq-Formel eingesetzt ergibt sich dann:
Damit hast du alle drei Nullstellen für diese Funktion bestimmt.
Wie hilfreich war dieser Beitrag?
Klicke auf die Sterne um zu bewerten!