Lineare Funktionen sind besonders einfache Funktionen. Sie ermöglichen dir ganz einfach einen Einstieg in das Verstehen von Zusammenhängen. Und sie kommen in Natur- und Sozialwissenschaften immer wieder vor, haben also eine hohe praktische Bedeutung. In diesem Artikel erfährst du alles, was du zu linearen Funktionen wissen musst.
Was sind lineare Funktionen?
Um ein erstes Verständnis zu linearen Funktionen zu erhalten (oder aufzufrischen), schaust du dir am besten das folgende Video an. Hier erklären wir dir, wozu du lineare Funktionen brauchst, wie du sie zeichnest und wie du eine Funktion aufstellen kannst.
[su_vimeo url=“https://vimeo.com/318057777″]
[su_box title=“Das Wichtigste in Kürze“ box_color=“#e35c37″ title_color=“#ffffff“]
Lineare Funktionen stellen lineare Zusammenhänge zwischen zwei Variablen her – wie zum Beispiel den Zusammenhang zwischen der Anzahl an Verkäufen eines bestimmten Produkts und dem mit diesem Produkt erzielten Umsatz. Alle linearen Funktionen haben die Form:![]() Im Koordinatensystem werden sie als Gerade dargestellt. x ist dabei die (unabhängige) Variable, die du verändern kannst (im Beispiel die Anzahl der Verkäufe), y der Wert, der sich daraus ergibt, der also von x abhängt und daher auch abhängige Variable heißt (der erzielte Umsatz). m ist die Steigung des Graphen und n der y-Achsenabschnitt, also der Abstand vom Nullpunkt zur Schnittstelle der Gerade mit der y-Achse.
Im Koordinatensystem werden sie als Gerade dargestellt. x ist dabei die (unabhängige) Variable, die du verändern kannst (im Beispiel die Anzahl der Verkäufe), y der Wert, der sich daraus ergibt, der also von x abhängt und daher auch abhängige Variable heißt (der erzielte Umsatz). m ist die Steigung des Graphen und n der y-Achsenabschnitt, also der Abstand vom Nullpunkt zur Schnittstelle der Gerade mit der y-Achse.
Eine typische lineare Funktion sieht wie folgt aus:
 Lineare Funktionen haben eine hohe praktische Bedeutung, weil sie in Natur- und Sozialwissenschaften eingesetzt werden können, um Zusammenhänge darzustellen und besser zu beleuchten.
Lineare Funktionen haben eine hohe praktische Bedeutung, weil sie in Natur- und Sozialwissenschaften eingesetzt werden können, um Zusammenhänge darzustellen und besser zu beleuchten.
[/su_box]
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=1]
[su_divider top=“no“ divider_color=“#eeeeee“]
Lineare Funktionen aufstellen und zeichnen – ein Beispiel
Im Beispiel sind lineare Funktionen am leichtesten zu verstehen. Daher zeigen wir dir hier zunächst einmal anhand einer praktischen Anwendung, wie du eine lineare Funktion zeichnest und wie du die zugehörige Gleichung bestimmen kannst.
Wertetabelle einer linearen Funktion
Wir bleiben bei dem Verkaufsbeispiel von oben. Luisa möchte sich ihr Taschengeld mit einem Limonaden-Stand aufbessern. Sie stellt selbst Limonade aus Wasser, Zitronen und Zucker her. Sie verkauft jedes Glas Limonade für 50 Cent. Sie kann also leicht ausrechnen, wie hoch ihre Einnahmen sind – abhängig von der Anzahl der verkauften Gläser. Sie stellt dafür zunächst eine Tabelle auf. Diese nennt man Wertetabelle, weil sie die unterschiedlichen Werte für Gläser und Einnahmen enthält. Luisas Wertetabelle sieht wie folgt aus:
| Verkaufte Gläser Limonade | Einnahmen (in Euro) |
| 1 | 0,50 |
| 2 | 1,00 |
| 3 | 1,50 |
| 4 | 2,00 |
| 5 | 2,50 |
| 6 | 3,00 |
Da Luisa zum ersten Mal Limonade verkauft, hat sie noch gar keine Vorstellung davon, mit welchen Verkäufen sie rechnen kann. Da in ihrer Straße gerade sonntags viele Spaziergänger unterwegs sind und das Wetter sehr schön werden soll, glaubt sie, dass sie sogar bis zu 50 Gläser verkaufen kann. Sie möchte die Wertetabelle aber nicht für jeden möglichen Wert ausrechnen, sondern sucht nach einer einfacheren Möglichkeit, ihre Einnahmen zu berechnen.
Die Funktion aufstellen
Zum Glück beschäftigt sie sich in der Schule gerade mit linearen Funktionen. So weiß Luisa, dass der Zusammenhang zwischen Gläsern und Einnahmen linear ist, denn mit jedem mehr verkauften Glas steigen die Einnahmen immer um den exakt selben Betrag. Pro Glas nimmt Luisa 50 Cent ein, sodass sie ganz einfach eine Funktion aufstellen kann. Dafür muss sie nur wissen, dass die Anzahl der verkauften Gläser die unabhängige Variable, also x, ist, denn diese weiß sie natürlich im Vorfeld noch nicht. Die Einnahmen sind also y. Mit jedem weiteren Glas nimmt Luisa 50 Cent mehr ein. Wenn die Funktion Euro darstellen soll, beträgt die Steigung (m) also 0,5. Luisas erste lineare Funktion hat daher die folgende Form:
![]() Luisa ist zufrieden und rechnet aus, dass sie bei 50 verkauften Gläsern 0,5 • 50 = 25 Euro einnimmt. Stolz zeigt sie das Ergebnis ihrer älteren Schwester Maja. Doch Maja erinnert Luisa daran, dass diese auch Ausgaben hatte für Zitronen und Zucker, die in jedem Fall ihre Einnahmen schmälern – egal, wie viel sie verdient. Luisa möchte auch das in der Funktion abbilden. Insgesamt hat sie 2,70 Euro ausgegeben. Da sie das Geld schon bezahlt hat und diese Kosten auf jeden Fall anfallen, zieht sie den Betrag von ihrer Funktion ab und erhält:
Luisa ist zufrieden und rechnet aus, dass sie bei 50 verkauften Gläsern 0,5 • 50 = 25 Euro einnimmt. Stolz zeigt sie das Ergebnis ihrer älteren Schwester Maja. Doch Maja erinnert Luisa daran, dass diese auch Ausgaben hatte für Zitronen und Zucker, die in jedem Fall ihre Einnahmen schmälern – egal, wie viel sie verdient. Luisa möchte auch das in der Funktion abbilden. Insgesamt hat sie 2,70 Euro ausgegeben. Da sie das Geld schon bezahlt hat und diese Kosten auf jeden Fall anfallen, zieht sie den Betrag von ihrer Funktion ab und erhält:
 Die lineare Funktion im Koordinatensystem darstellen
Die lineare Funktion im Koordinatensystem darstellen
Diese Funktion bildet nicht nur Luisas Einnahmen, sondern ihren Gewinn ab. Luisa möchte wissen, wie viele Gläser sie verkaufen muss, um ihre Ausgaben auszugleichen. Dies kann man ausrechnen oder zeichnerisch lösen. Luisa entscheidet sich für die zweite Variante und trägt die Funktion im Koordinatensystem ab. Dafür berechnet sie die Werte für zwei Punkte. Da sie ihre Funktion verändert hat, kann sie ihre ursprüngliche Wertetabelle nicht mehr nehmen, sondern ermittelt zwei neue Punkte der Gerade.
| x | y |
| 1 | 0,5 • 1 – 2,7 = -2,2 |
| 2 | 0,5 • 2 – 2,7 = -1,7 |
Diese beiden Punkte trägt Luisa in ein Koordinatensystem ein – die x-Werte auf der x-Achse (waagerecht) und die y-Werte auf der y-Achse (senkrecht). Diese beiden Punkte verbindet sie dann und zieht eine Gerade hindurch.
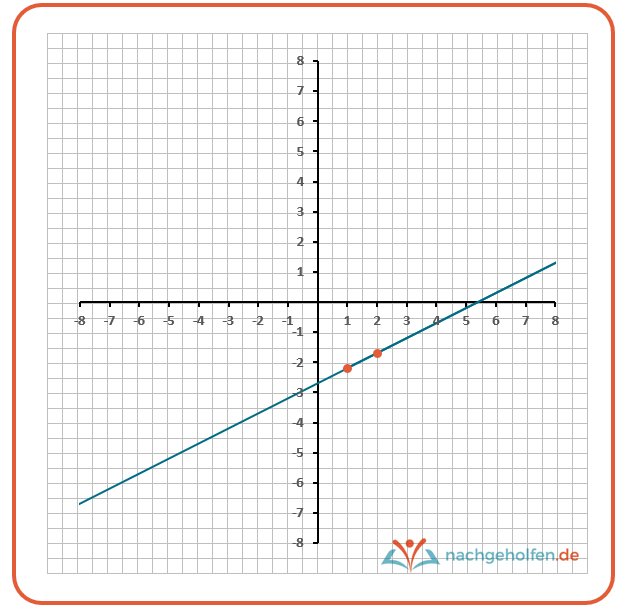 Luisa erkennt, dass ihre Gerade die x-Achse zwischen 5 und 6 schneidet. Ab dieser Stelle nimmt die Funktion nur noch positive Werte an. Ab dem 6. verkauften Glas kann Luisa ihre Kosten also decken.
Luisa erkennt, dass ihre Gerade die x-Achse zwischen 5 und 6 schneidet. Ab dieser Stelle nimmt die Funktion nur noch positive Werte an. Ab dem 6. verkauften Glas kann Luisa ihre Kosten also decken.
 Lineare Funktionen erklärt
Lineare Funktionen erklärt
Du hast im Beispiel bereits gesehen, was lineare Funktionen sind und wie du mit ihnen Sachverhalte darstellen kannst. Im Folgenden erklären wir dir das gesamte Hintergrundwissen zu linearen Funktionen, dass du für die Schule wissen solltest.
Grundlagen linearer Funktionen
Wie oben bereits beschrieben hat eine lineare Funktion hat die Form fx = mx + n bzw. y = mx + n mit m,n ∈ R. m,n ∈ R bedeutet, dass m und n relle Zahlen sind. Für dich wird das wahrscheinlich keinerlei Auswirkungen haben, weil du in der Schule ohnehin nur mit reellen Zahlen arbeitest. Grundsätzlich ist diese Information aber wichtig, da man beispielsweise mit komplexen Zahlen keine linearen Funktionen erstellen kann.
„linear“ bedeutet „gerade“ oder „geradlinig“, und lineare Funktionen werden im Koordinatensystem immer als Gerade dargestellt, die du mit dem Lineal zeichnen kannst – so kannst du dir diesen Begriff merken. Ist die Funktion keine Gerade, so ist sie nicht linear.
Lineare Funktionen für n = 0
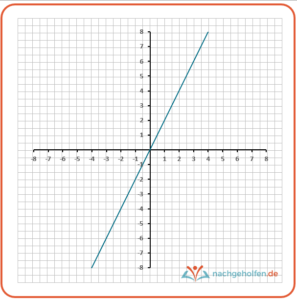 Sowohl m als auch n können übrigens gleich Null sein, und trotzdem bleibt die Funktion linear. Ist n gleich Null, so verläuft die Gerade durch den Ursprung (= Nullpunkt) des Koordinatensystems. Jeder Wert wird also auf sein eigenes Vielfaches abgebildet.
Sowohl m als auch n können übrigens gleich Null sein, und trotzdem bleibt die Funktion linear. Ist n gleich Null, so verläuft die Gerade durch den Ursprung (= Nullpunkt) des Koordinatensystems. Jeder Wert wird also auf sein eigenes Vielfaches abgebildet.
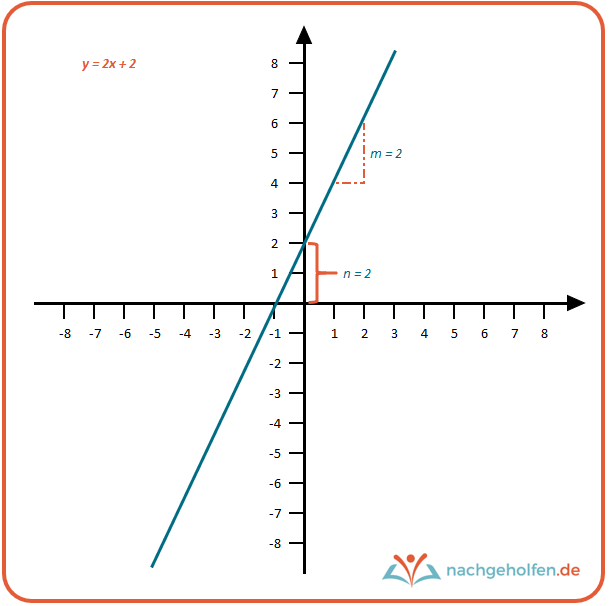
Man spricht daher auch von proportionalen Funktionen, die einen Sonderfall von linearen Funktionen darstellen. Im Bild siehst du den Graphen der proportionalen Funktion y = 2x. Hier wird jedem Wert sein doppelter Wert zugeordnet. Du könntest die Funktion entsprechend auch ganz einfach „Verdoppeln“ nennen, denn du verdoppelst x, um den Wert für y auszurechnen und im Koordinatensystem an der richtigen Stelle einzutragen.
Lineare Funktionen für m = 0
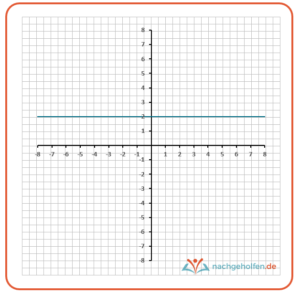 Ist m gleich Null, so verändert sich der Wert der Funktion nicht, egal, welchen Wert für x du einsetzt. Das hat als Folge, dass die Gerade eine Parallele zur x-Achse wird.
Ist m gleich Null, so verändert sich der Wert der Funktion nicht, egal, welchen Wert für x du einsetzt. Das hat als Folge, dass die Gerade eine Parallele zur x-Achse wird.
Übrigens kann eine Funktion nie eine Parallele zur y-Achse sein. Auch wenn du eine solche Parallele mit dem Lineal zeichnen würdest, handelt es sich dabei nicht um eine lineare Funktion, ja, nicht einmal um eine Funktion. Denn eine Funktion ordnet jedem Wert von x eindeutig einen y-Wert zu. Das wäre bei einer Parallelen zur y-Achse nicht mehr gegeben. Hier würden einem x-Wert unendlich viele verschiedene y-Werte zugeordnet.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=2]
[su_divider top=“no“ divider_color=“#eeeeee“]
Die einzelnen Elemente einer linearen Funktion
Du kennst nun schon die grundlegenden Elemente einer linearen Funktion. Zu m und n gibt es noch einiges mehr zu wissen, was du im Folgenden nachlesen kannst. Wir schreiben hier y = mx + n bzw. f(x) = mx + n. Dies sind übliche Schreibweisen. Genauso kommen aber auch zum Beispiel y = ax + b oder f(x) = ax + b und andere Schreibweisen vor. Dies macht in der Sache keinen Unterschied, weil es ja um die Zusammenhänge geht und die Buchstaben nur Platzhalter sind. Daher solltest du in der Schule immer die Bezeichnungen wählen, die ihr auch dort gelernt habt, damit du nicht durcheinander kommst.
Die Steigung der linearen Funktion: m
Schon am Namen der Steigung kannst du feststellen, was sie aussagt: Sie gibt an, wie die Funktion verläuft. Wenn deine lineare Funktion eine Steigung von 1 hat (also y = x + n, die 1 als Koeffizient schreibt man dann nicht mehr ausdrücklich hin), verläuft sie auf oder parallel zur Hauptdiagonalen des Koordinatensystems. Ist m größer als 1, verläuft die Funktion entsprechend steiler, ist sie kleiner als 1, flacher. Ein positives m zeigt an, dass die Funktion steigt. Das bedeutet, dass mit zunehmendem x auch die y-Werte immer größer werden. Ist m dagegen kleiner als x, fällt die Funktion. Dies sieht man auch im Graphen, der in diesem Fall von links nach rechts abfällt.
Die Steigung im Graphen ablesen
Im Beispiel oben hat Luisa pro Glas Limonade 50 Cent bzw. 0,5 Euro eingenommen. Die Steigung m der linearen Funktion ist also 0,5, denn mit jedem weiteren verkauften Glas steigen Luisas Einnahmen um 0,5 Euro. Wir haben dies als Gerade eingezeichnet, obwohl das eigentlich inhaltlich nicht ganz korrekt ist. Denn Luisa verkauft ja nur ganze Gläser Limonade, und nicht zum Beispiel 5,4. Das ist bei der Darstellung von Zusammenhängen als Funktionen leider häufig der Fall. Bei der Interpretation solltest du dies im Hinterkopf behalten.
Im obigen Beispiel wissen wir die Steigung der Funktion aus Luisas Kalkulation. Du könntest sie aber auch umgekehrt aus der Funktion ablesen, und zwar über ein sogenanntes Steigungsdreieck.
Das Steigungsdreieck einer linearen Funktion ist ein rechtwinkliges Dreieck, das besteht aus:
- einem Abschnitt der Geraden,
- einer Parallele zur x-Achse und
- einer Paralle zur y-Achse, alle drei verbunden zu einem Dreieck.
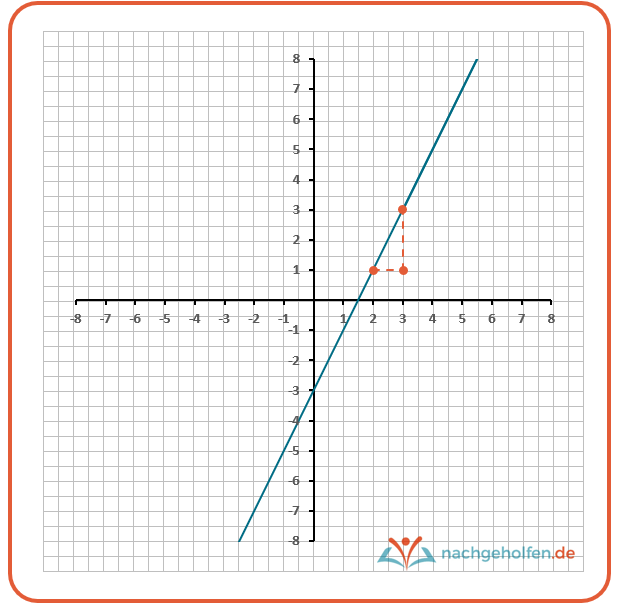
In der folgenden Graphik ist das Steigungsdreieck abgetragen. Die Steigung kannst du dann ganz einfach ausrechnen, indem du die Veränderung auf der y-Achse (2 Schritte nach oben) durch die Veränderung auf der x-Achse (1 Schritt nach rechts) teilst. m entspricht hier also 2. Mathematisch formuliert sieht dies so aus:
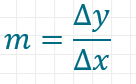
Die Steigung aus zwei Punkten der linearen Funktion berechnen
Es ist nicht immer ganz einfach, die Steigung aus dem Graphen abzulesen, vor allem, wenn es sich dabei nicht um den Quotienten von ganzen Zahlen handelt. Außerdem musst du in manchen Aufgaben gezielt m aus zwei gegebenen Punkten einer linearen Funktion berechnen, ohne diese erst zu zeichnen. Das ist sehr einfach möglich, denn genauso wie du das Steigungsdreieck an jede Stelle der linearen Funktion anzeichnen kannst, kannst du aus zwei beliebigen Punkten der Funktion die Steigung berechnen. Da eine lineare Funktion eine Gerade ist, ist die Steigung überall gleich, sodass es egal ist, welche zwei Punkte du nimmst.
Aus zwei Punkten berechnest du die Steigung der linearen Funktion wie folgt:
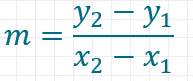
Natürlich muss es sich bei diesen beiden Punkten um zwei unterschiedliche Punkte auf der Funktion handeln, da du sonst keine Steigung aus ihnen berechnen kannst.
Wir überprüfen dies wieder an Luisas Funktion. Luisa hat bereits zwei Punkte ausgerechnet, um die Gerade zeichnen zu können, den Punkt (1|-2,2) und den Punkt (2|-1,7). Daraus berechnen wir nun mit der obigen Formel die Steigung m. Dafür musst du nur wissen, dass die Punkte in der Form (x|y) aufgeschrieben sind. Der erste Wert ist also immer der x-Wert, der zweite der y- Wert. Das bedeutet also:
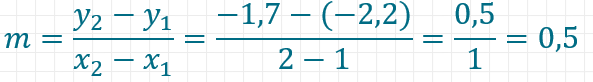
Die Steigung in Luisas Funktion ist also m = 0,5. Alles andere hätte uns jetzt auch überraschen müssen. Du erhältst übrigens dasselbe Ergebnis, wenn du die Punkte umdrehst, wenn du also (1|-2,2) als zweiten und (2|-1,7) als ersten Punkt verwendest.
Der Achsenabschnitt oder Verschiebungskonstante: n
Luisa hat zunächst nur ihre Einnahmen gezählt, bis ihre Schwester sie daran erinnert hat, dass sie auch Kosten für die Limonade hatte. Diese hat Luisa einfach von der Funktion abgezogen. In der Graphik bedeutet dies, dass die ursprüngliche Gerade (y= 0,5x) um -2,7 verschoben wird, also 2,7 Einheiten nach unten. -2,7 ist daher die sogenannte Verschiebungskonstante bzw. der y-Achsenabschnitt. Denn bei -2,7 schneidet die Gerade der Funktion die y-Achse. Dies kannst du ganz einfach in der Graphik ablesen. In der Funktion y = mx + n ist er das n.
So berechnest du den y-Achsenabschnitt aus m und einem Punkt
Du kannst den y-Achsenabschnitt natürlich aus der Graphik ablesen. Du kannst ihn aber auch ebenso gut berechnen. Dafür brauchst du nur die Steigung m und einen beliebigen Punkt der Funktion.
Die Funtionsgleichung von Luisas Funktion ist y = 0,5x -2,7 Nehmen wir an, wir wüssten noch nicht, wie viel Luisa ausgegeben hat und hätten bisher nur die Information, dass sie für jedes Glas Limonade 0,5 Euro einnimmt. Die Gleichung würde dann so aussehen: y = 0,5x + n. n müssen wir nun ausrechnen. Wir können die Gleichung ganz einfach umformen zu n = y – 0,5x. (Tipp: Hier erfährst du, wie du Gleichungen umformen kannst.)
Jetzt wissen wir, dass Luisa bei einem Glas Limonade einen Verlust von 2,20 Euro macht. Wir können also einsetzen:
n = -2,2 – 0,5 • 1 = – 2,7
und schon haben wir den y-Achsenabschnitt errechnet.
Schnittpunkte mit den verschiedenen Achsen
Schnittpunkt mit der y-Achse
Der Schnittpunkt einer Gerade mit der y-Achse ist – wie oben bereits erwähnt – der y-Achsenabschnitt oder n. Aus der Funktionsgleichung kannst du diesen Schnittpunkt also einfach ablesen. Achte dabei nur darauf, dass du auch das Vorzeichen von n berücksichtigst!
Alternativ kannst du den Schnittpunkt mit der y-Achse auch in der Funktionsgraphik ablesen. Egal, wie du den Punkt ermittelst, er wird geschrieben als (n|0).
Schnittpunkt mit der x-Achse
Solange deine Funktion eine Steigung ungleich Null hat, wird sie an irgendeinem Punkt die x-Achse schneiden. Den Schnittpunkt kannst du natürlich auch aus der Graphik ablesen, oder du rechnest ihn durch Umformungen aus.
Der Schnittpunkt mit der x-Achse hat oft auch eine wichtige inhaltliche Aussagekraft. Für Luisa ist es der Punkt, ab dem sie keinen Verlust mehr mit ihrem Limonadenstand macht. Natürlich möchte sie wissen, ab wann das der Fall ist.
Sie kann den genauen Wert einfach ausrechnen, indem sie für y 0 in die Gleichung einsetzt und dann die Gleichung nach x auflöst.
0 = 0,5•x – 2,7
2,7 = 0,5x
0,5x = 2,7
x = 5,4
Ab 5,4 Gläsern macht Luisa also rechnerisch keinen Verlust mehr. Da sie nur ganze Gläser verkauft, ist das 6. Glas das erste, mit dem sie ein bisschen Gewinn macht.
Analytische Eigenschaften von linearen Funktionen
Lineare Funktionen kannst du natürlich auch im Rahmen der Kurvendiskussion untersuchen. Sie sind stetig und differenzierbar. Die wichtigsten Eigenschaften findest du im Folgenden.
Ableitung und Stammfunktion
Die Ableitung von fx = mx + n ist f‘x = m. Mit der ersten Ableitung erhältst du also die Steigung.
Die Stammfunktion von fx = mx + n ist Fx = m/2x2 + nx +c
Grenzwerte
Die Grenzwerte einer linearen Funktion hängen davon ab, ob m größer oder kleiner als Null ist.
Ist m positiv, so strebt die Funktion nach unendlich für unendlich große x und nach -unendlich für unendlich kleine x. Graphisch ist das daran erkennbar, dass der Graph sich von unten links nach oben rechts entwickelt (wie im Luisa-Beispiel).
Ist m negativ, so ist der Verlauf umgekehrt. Je größer x wird, desto kleiner wird der Funktionswert, die Funktion fällt also von links oben nach rechts unten ab.
Ist die Steigung der linearen Funktion gleich Null, so läuft der Graph parallel zur x-Achse und die Grenzwerte sind gleich dem Wert von n. Dies ist jedoch ein Sonderfall, der nur selten in Schulaufgaben vorkommt.
3 Beispielaufgaben mit Lösungen zu linearen Funktionen
Aufgabe 1: Funktionsgleichung aus Steigung und Punkt ermitteln
Die Steigung einer linearen Funktion ist m = 1,2. Auf der Geraden liegt der Punkt P (15|20). Wie lautet die zugehörige Funktionsgleichung?
Um diese Aufgabe zu lösen, musst du zunächst überlegen, was dir für die Aufstellung der Funktion fehlt. Die Funktionsgleichung lautet immer y = mx + n, m kennst du bereits, also fehlt dir noch n.
Du kennst bereits einen Punkt auf der Geraden. Diesen kannst du in die Funktionsgleichung, die du bisher kennst, einsetzen und dann nach n auflösen, also:
y = 1,2x + n
20 = 1,2•15 + n
20 = 18 + n
2 = n
n = 2
Du kennst nun m und n und kannst die Funktionsgleichung aufstellen. Sie lautet:
y = 1,2x + 2.
Aufgabe 2: Funktionsgleichung aus zwei Punkten ermitteln
Du weißt, dass die Punkte (2|19) und (3|26) auf einer Geraden liegen. Ermittle die Gleichung für die lineare Funktion, die durch beide Punkte verläuft.
Auch hier fragst du dich zunächst, was dir fehlt. Leider kennst du weder m noch n, sodass dir beides noch fehlt und du beide Konstanten nacheinander berechnen musst.
Am besten fängst du hier mit der Steigung m an. Weiter oben haben wir dir gezeigt, wie du die Steigung einer Funktion ganz einfach aus zwei Punkten berechnen kannst. Hier noch einmal die Formel dazu:
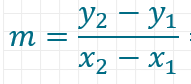
In diese Formel setzt du die beiden Punkte ein:
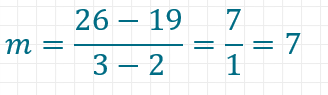
Wenn du m kennst, kannst du wie in der letzten Aufgabe einen der Punkte und die Steigung verwenden, um n zu berechnen.
y = 7x + n
26 = 7•3 + n
26 = 21 + n
5 = n
n = 5
Die Funktionsgleichung lautet also y = 7x + 5. Selbstverständlich hättest du dasselbe Ergebnis erhalten, wenn du n mit Hilfe des anderen Punkts berechnet hättest.
Aufgabe 3: Schnittpunkt zweier Geraden ermitteln
In welchem Punkt schneiden sich die beiden Geraden y = 2x + 2 und y =-x + 2,6?
Diese Aufgabe ist ein wenig anders als die ersten beiden, du kannst sie aber mit dem Handwerkszeug, das du bisher erlernt hast, leicht lösen. Der Schnittpunkt der beiden Geraden zeichnet sich ja dadurch aus, dass sie an dieser Stelle denselben x-Wert und denselben y-Wert annehmen. Also kannst du die beiden Gleichungen im ersten Schritt einfach gleichsetzen und so x ausrechnen. Das sieht dann wie folgt aus:
2x + 2 = x +2,6
x = 0,6
x setzt du nun in eine beliebige der beiden Gleichungen ein. Beide müssen ja dasselbe Ergebnis für y ergeben, weil die beiden Geraden sich an dieser Stelle schneiden.
y = 2•0,6 + 2 = 3,2
Der Schnittpunkt der beiden Geraden liegt also bei (0,6|3,2). Du könntest ihn auch aus der Graphik ablesen.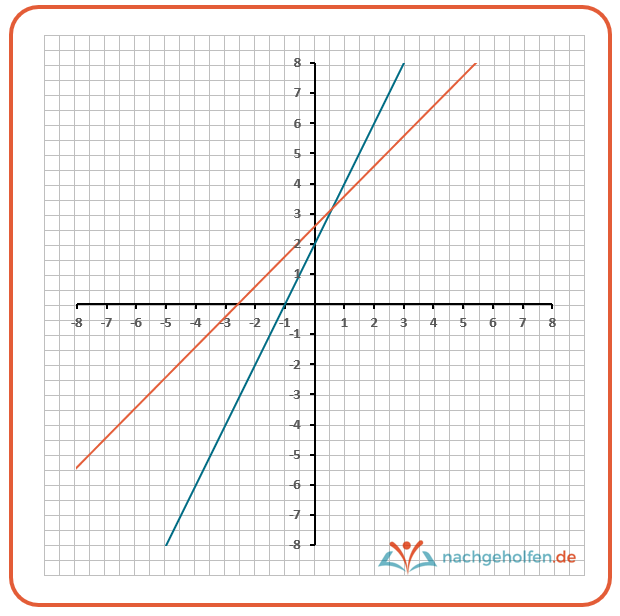
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=3]
[su_divider top=“no“ divider_color=“#eeeeee“]
Die wichtigsten Fragen zu linearen Funktionen beantwortet
Wenn du noch Fragen zu linearen Funktionen hast, wirst du in dieser Übersicht sicher fündig. Falls nicht, schreibe uns gerne eine E-Mail oder einen Kommentar!
[su_accordion]
[su_spoiler title=“Welche Bestandteile hat eine lineare Funktion?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Um eine lineare Funktion aufzustellen, benötigst du die Steigung m und den y-Achsenabschnitt n. x und y sind Variablen, für sie brauchst du keinen Wert. Für x setzt du nämlich verschiedene Werte ein und y ergibt sich aus der Gleichung.[/su_spoiler]
[su_spoiler title=“Was ist die Punktprobe für eine lineare Funktion?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Mit der Punktprobe kannst du feststellen, ob ein Punkt auf der Funktionsgeraden liegt oder nicht. Dies kannst du sehr leicht graphisch erkennen. Du kannst aber auch den x-Wert des Punkts in die Funktionsgleichung einsetzen. Ergibt die Funktionsgleichung den y-Wert des Punkts, so liegt dieser auf der Geraden, sonst nicht.
[/su_spoiler]
[su_spoiler title=“Welche Anwendungen gibt es für lineare Funktionen?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Lineare Funktionen werden in den WIrtschafts-, Natur- und Sozialwissenschaften angewendet. Überall, wo zwei Dinge linear zusammenhängen, kannst du lineare Funktionen anwenden. Wenn du Aufgaben für die Anwendung suchst, schaue dir am besten unsere Arbeitshefte zu dem Thema an.
[/su_spoiler]
[su_spoiler title=“Welche linearen Funktionen haben keine Nullstelle?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Nur lineare Funktionen, die parallel zur x-Achse verlaufen, haben keine Nullstelle. Ist die Gerade nicht parallel zur x-Achse, so wird sie diese irgendwann schneiden – dort liegt dann die Nullstelle. Für lineare Funktionen ohne Nullstelle ist m daher immer gleich Null, die Funktionsgleichung lautet also y = n.
[/su_spoiler]
[su_spoiler title=“Wie viele Nullstellen hat eine lineare Funktion?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Eine lineare Funktion hat maximal eine Nullstelle. Verläuft die Funktion nicht parallel zur x-Achse, so schneidet sie diese an genau einer Stelle. Da die Funktion ja linear ist, also nie ihre Richtung ändert, kann sie die x-Achse kein zweites Mal schneiden und es gibt auch nicht mehr als eine Nullstelle.
[/su_spoiler]
[su_spoiler title=“Welche charakteristischen Eigenschaften hat eine lineare Funktion?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Eine lineare Funktion ist eine Gerade. Du kannst sie also mit dem Lineal zeichnen. Sie hat keine Wendepunkte und maximal eine Nullstelle. Sie schneidet die y-Achse an genau einer Stelle, und zwar am sogenannten y-Achsenabschnitt.
[/su_spoiler]
[su_spoiler title=“Welche linearen Funktionen verlaufen durch den Ursprung?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Der Ursprung des Koordinatensystems ist der Nullpunkt, also der Punkt, an dem x und y gleich Null sind. Das bedeutet, dass nur lineare Funktionen durch den Ursprung verlaufen, deren y-Achsenabschnitt gleich Null ist, weil alle anderen Funktionen nach oben oder unten verschoben sind. Der y-Achsenabschnitt wird durch n angegeben. Die Gleichung für lineare Funktionen durch den Ursprung lautet also: y = mx. Dies sind proportionale Funktionen, eine Sonderform linearer Funktionen.
[/su_spoiler]
[su_spoiler title=“Was ist der Unterschied zwischen linearen Gleichungen und linearen Funktionen?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Rein mathematisch gibt es keinen großen Unterschied. Die Gleichung, die eine lineare Funktion beschreibt, ist immer eine lineare Gleichung. Eine Funktion zeigt jedoch alle Paare von x und y an, die auf einer Geraden liegen und durch die Funktionsgleichung beschrieben werden. Wenn du eine lineare Gleichung lösen sollst, suchst du meist x für ein bestimmtes y.
Die Gleichung zu einer linearen Funktion lautet also zum Beispiel y = 3x – 2. Dies ist gleichzeitig auch eine lineare Gleichung mit unendlich vielen Lösungen, die alle auf der Funktionsgeraden liegen. Üblicherweise wirst du aber lineare Gleichungen in der Form 3 x – 2 = 10 lösen sollen, die dann einen bestimmten Punkt auf der Gerade bestimmen.
[/su_spoiler]
[su_spoiler title=“Wie kann man lineare Funktionen verschieben?“ open=“no“ style=“default“ icon=“plus“ anchor=““ class=““]
Lineare Funktionen verschiebt man rechnerisch, indem man n ändert. Sollst du beispielsweise die Funktion y = 3x + 2 um eine Einheit nach oben verschieben, so zeichnest du y = 3x + 3. Im Koordinatensystem kannst du einfach die Gerade mit Hilfe deines Geodreicks parallel um eine Einheit verschieben.
[/su_spoiler]
[/su_accordion]
Zusammenfassung
[featured_snippet image=“https://nachgeholfen.de/wp-content/uploads/2019/02/Lineare-Funktionen-Graph_klein.png“ image_alt=“So zeichnest du lineare Funktionen“]
Eine lineare Funktion hat die Form y = mx + n.
Im Koordinatensystem werden lineare Funktionen als Gerade dargestellt.
Die einzelnen Elemente einer linearen Funktion sind:
- y: Funktionswert, unabhängige Variable
- x: abhängige Variable der Funktion
- m: Steigung
- n: y-Achsenabschnitt
Lineare Funktionen werden verwendet, um zum Beispiel in den Sozial- und Naturwissenschaften lineare Zusammenhänge darzustellen und zu untersuchen.
[/featured_snippet]
Du suchst nach noch mehr Übungen und Aufgaben für lineare Funktionen? Die findest du in unseren Arbeitsheften zum Thema. Unsere Online-Nachhilfe unterstützt dich außerdem ganz individuell beim Lernen.
[su_box title=“Tipp! Mach dich jetzt fit für die Klausur mit unseren Arbeitsheften:“ box_color=“#006c84″ title_color=“#ffffff“]
[/su_box]Konnten wir dir mit unserem Artikel helfen? Wir freuen uns über deine Bewertung und Kommentare!
[yasr_visitor_votes size=“medium“]