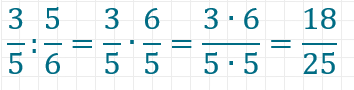In der Mathematik werden verschiedene Zahlbereiche unterschieden, zu denen Zahlen nach einer bestimmten Definition gezählt werden. Solche Zahlbereiche sind zum Beispiel natürliche Zahlen oder ganze Zahlen. Ein weiterer Zahlbereich sind die rationalen Zahlen, um die es in diesem Artikel geht.
Was sind rationale Zahlen?
Rationale Zahlen sind alle Zahlen, die man als Verhältnis zweier ganzer Zahlen zueinander schreiben kann. Die Bezeichnung stammt vom Lateinischen Wort „ratio“, was unter anderem „Verhältnis“ heißt. Die Menge aller rationalen Zahlen wird mit einem ℚ mit Doppelstrich bezeichnet. Das Q kommt von Quotient, also vom Ergebnis der Division.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=1]
[su_divider top=“no“ divider_color=“#eeeeee“]
Eine andere Bezeichnung für rationale Zahlen lautet Bruchzahlen, denn Brüche sind nichts anderes als die Darstellung von Verhältnissen zweier Zahlen. Der Begriff rationale Zahlen ist jedoch der in der Mathematik gebräuchlichere, denn es zählen ja nicht nur alle Brüche, sondern auch alle Zahlen, die als Brüche geschrieben werden können zu den rationalen Zahlen. Da zum Beispiel alle ganze Zahlen als Bruch mit dem Nenner 1 geschrieben werden können, sind auch sie Bestandteil der rationalen Zahlen, obwohl man sie nicht auf den ersten Blick als Bruchzahlen erkennen kann. Darüber hinaus können Bruchzahlen auch nicht-ganze Zahlen als Zähler oder Nenner haben, und so lassen sich auch Zahlen als Brüche darstellen, die nicht unbedingt rationale Zahlen sind.
Da rationale Zahlen oft als Brüche dargestellt werden, ist es wichtig, dass du die Grundbegriffe hierzu kennst. Jeder Bruch wird wie folgt dargestellt:
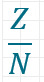
Der Strich in der Mitte heißt Bruchstrich und er bedeutet genau dasselbe wie das Teilungszeichen :. Die Zahl über dem Bruchstrich (Z) wird also durch die Zahl unter dem Bruchstrich (N) geteilt. Beide Zahlen haben spezifische Bezeichnungen. Z ist der Zähler und N ist der Nenner des Bruchs. Du kannst dir das so merken, dass N angibt, wie der Bruch bezeichnet wird.

wird zum Beispiel „ein Achtel“ ausgesprochen, das „Achtel“ kommt also vom Nenner 8). Und mit dem Zähler kannst du diesen Bruch entsprechend weiter zählen, also ein Achtel, zwei Achtel, drei Achtel und so weiter.
Wie du mit rationalen Zahlen rechnen kannst
Brüche erweitern und kürzen
Eine ganz einfache Operation, die man mit allen rationalen Zahlen durchführen kann, ist das Erweitern eines Bruchs. Dabei multiplizierst du einfach Zähler und Nenner mit derselben ganzen Zahl. Der Wert des Bruchs bleibt dabei unverändert, das heißt:
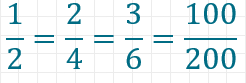
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=2]
[su_divider top=“no“ divider_color=“#eeeeee“]
Wenn du diese Operation umgekehrt durchführst, also Zähler und Nenner durch dieselbe ganze Zahl teilst, spricht man vom Kürzen. Kürzen kannst du einen Bruch nur dann, wenn Zähler und Nenner einen gemeinsamen Teiler besitzen. Wenn du in einer Klassenarbeit mit rationalen Zahlen rechnest und eine Bruchzahl als Ergebnis erhältst, solltest du diese immer so weit kürzen, bis es nicht mehr geht. Hierzu nutzt du den größten gemeinsamen Teiler von Zähler und Nenner.
Addition und Subtraktion von rationalen Zahlen
Um rationale Zahlen addieren oder subtrahieren zu können, müssen sie denselben Nenner haben. Oft haben sie das nicht von Anfang an, sodass du einen oder beide Brüche zunächst auf das kleinste gemeinsame Vielfache erweitern musst und anschließend das Ergebnis ausrechnen kannst.
Beispiel für eine Addition:
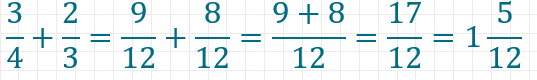
Dasselbe gilt natürlich auch für rationale Zahlen, die gar nicht als Brüche dargestellt sind, wie das folgende Beispiel zeigt.
Beispiel für eine Subtraktion:
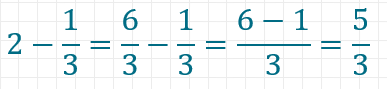
Multiplikation von rationalen Zahlen
Du kannst Brüche ganz einfach multiplizieren, indem du die beiden Zähler miteinander multiplizierst und die beiden Nenner ebenfalls, wie im unten stehenden Beispiel gezeigt.
Beispiel für eine Multiplikation:

[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=3]
[su_divider top=“no“ divider_color=“#eeeeee“]
Division von rationalen Zahlen
Die Division von Bruchzahlen ist ähnlich einfach wie die Multiplikation. Um einen Bruch durch einen anderen zu teilen, multiplizierst du einfach den ersten mit dem Kehrwert des zweiten.
Beispiel für eine Division: