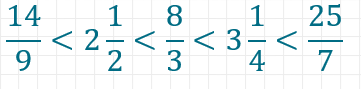In diesem Artikel erklären wir dir, wie du das kleinste gemeinsame Vielfache (kgV) von zwei Zahlen finden kannst. Das brauchst do vor allem dann, wenn du in der Bruchrechnung nach gemeinsamen Nennern von zwei oder mehr Brüchen suchst. Hier findest du eine übersichtliche Erklärung mit Beispielen und mit Video.
Was ist das kleinste gemeinsame Vielfache (kgV)?
Was das kleinste gemeinsame Vielfache zweier (oder mehr) Zahlen ist, erschließt sich eigentlich schon aus dem Namen.
Dieser besteht aus drei Teilen:
Vielfache einer Zahl sind alle anderen Werte, die du durch Multiplikation der Ausgangszahl mit einer anderen erhältst. Vielfache von 2 sind zum Beispiel 2, 4, 6, 8, 10, 12, 14, 16, 18, … Auch die 2 selbst ist ein Vielfaches der 2, da 1 • 2 = 2 gilt.
Wenn du die Vielfachen zweier Zahlen miteinander vergleichst, kannst du die Vielfachen feststellen, die beide gemeinsam haben. Die Vielfachen von 3 sind 3, 6, 9, 12, 15, 18, … 6, 12 und 18 sind also schon mal drei gemeinsame Vielfache von 2 und 3.
Das kleinste gemeinsame Vielfache davon ist die 6.
[su_divider top=“no“ divider_color=“#eeeeee“]
[su_divider top=“no“ divider_color=“#eeeeee“]
Wozu brauchst du das kleinste gemeinsame Vielfache?
Das kgV benötigst du vor allem beim Bruchrechnen. Damit du Brüche addieren, subtrahieren oder miteinander vergleichen kannst, müssen sie denselben Nenner haben. Du musst die Brüche also auf einen gemeinsamen Nenner erweitern.
Manchmal ist offensichtlich, was der gemeinsame Nenner ist, weil er sich ganz einfach aus dem kleinen Einmaleins ergibt, zum Beispiel hier:
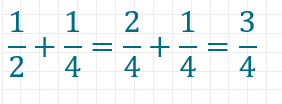
Da du weißt, dass 2 ein Teiler von 4 ist, ist es ganz einfach, die Brüche anzugleichen.
Auch in der folgenden Aufgabe kannst du das sehr wahrscheinlich intuitiv.
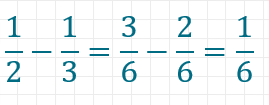
Wenn du jedoch mehrere Brüche hast, bei denen du nicht sofort erkennen kannst, welches der gemeinsame Nenner sein könnte, hast du grundsätzlich zwei Möglichkeiten, um sie auf einen Nenner zu bringen.
- Du multiplizierst einfach alle einzelnen Nenner miteinander und nimmst das Ergebnis als gemeinsamen Nenner. Dann weißt du, dass du jeden Bruch auf diese Zahl erweitern kannst. Sehr wahrscheinlich ist die Zahl aber dann größer als nötig, weil du schon einen kleineren gemeinsamen Nenner finden könntest. Daher ist die zweite Methode normalerweise diejenige, die man anwendet.
- Du suchst das kleinste gemeinsame Vielfache und nimmst dieses als gemeinsamen Nenner.
Wie du das kgV berechnest
Das kleinste gemeinsame Vielfache findest du in drei Schritten, indem du
- eine Primfaktorzerlegung für jeden einzelnen Wert vornimmst, ihn also als Produkt von einzelnen Primzahlen schreibst,
- wenn eine Primzahl in einem Produkt mehrfach vorkommst, sie nur einmal, aber mit Exponent schreibst,
- alle unterschiedlichen Primzahlen, die vorkommen, miteinander multiplizierst. Kommen Primzahlen mehrfach und mit unterschiedlichen Exponenten vor, nimmst du nur die mit dem höchsten Exponenten.
[su_divider top=“no“ divider_color=“#eeeeee“]
[su_divider top=“no“ divider_color=“#eeeeee“]
Beispielaufgabe 1
Finde das kleinste gemeinsame Vielfache der Zahlen 12, 14 und 15.
Schritt 1: Primfaktorzerlegung
Um eine Primfaktorzerlegung dieser drei Zahlen vorzunehmen, musst du natürlich wissen, welche Zahlen Primzahlen sind. Du brauchst allerdings immer nur die Primzahlen bis zur größten der Zahlen, für die du das kgV suchst, zu kennen. Hier findest du eine Übersicht über die Primzahlen bis 10.000, was dir wahrscheinlich für alle Aufgaben reichen wird. Die Primzahlen bis 20 (vielleicht auch bis 50) solltest du auswendig kennen. So viele brauchen wir für die Aufgabe aber gar nicht. Die Zahlen oben kannst du folgendermaßen in Primzahlen zerlegen:
12 = 2 • 2 • 3 = 22 • 3
14 = 2 • 7
15 = 3 • 5
Schritt 2: Identifizierung der einzelnen Primzahlen
Die einzelnen Primzahlen, die in den verschiedenen Zerlegungen vorkommen, sind 2, 3, 5 und 7. Diese multiplizierst du miteinander, und zwar immer mit dem höchsten vorkommenden Exponenten. Da bei der Primzahlzerlegung der 12 die 2 mit Exponent 2 vorkommt, ist das kgV dieser drei Zahlen:
Schritt 3: Multiplikation
22 • 3 • 5 • 7 = 420
Zur Probe kannst du noch das Ergebnis noch durch die einzelnen Zahlen teilen.
420 : 12 = 35
420 : 12 = 30
420 : 12 = 28
Übrigens sind alle Vielfachen des kgV ebenfalls Vielfache aller drei Zahlen.
Beispielaufgabe 2
Sortiere die folgenden Brüche der Größe nach in aufsteigender Reihenfolge:
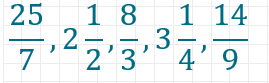
Schritt 1: Gemischte Zahlen in Brüche umrechnen
Um die Brüche vergleichbar zu machen, rechnen wir zunächst die beiden gemischten Zahlen in Bruchzahlen um. Dazu multiplizieren wir die ganze Zahl, die vor dem Bruch steht, mit dem Nenner des Bruchs, und addieren das Ergebnis zum Zähler, um den neuen Zähler zu erhalten. Die Brüche, die wir miteinander vergleichen werden, lauten jetzt also:
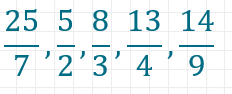
Nun suchen wir den gemeinsamen Nenner der Brüche, also das kleinste gemeinsame Vielfache der Zahlen 7, 2, 3, 4 und 9.
Schritt 2: Primfaktorzerlegung
Wir müssen hier zwar für insgesamt fünf Zahlen eine Primfaktorzerlegung vornehmen, aber die ersten drei sind bereits Primzahlen, sodass dieser Schritt sehr schnell geht.
7 = 7
2 = 2
3 = 3
4 = 2 • 2 = 22
9 = 3 • 3 = 32
Schritt 3: Identifizierung der einzelnen Primzahlen
Wie auch in der ersten Aufgabe müssen wir nun alle vorkommenden Primzahlen mit höchstem Exponenten identifizieren. Dies sind 22, 32 und 7.
[su_divider top=“no“ divider_color=“#eeeeee“]
[su_divider top=“no“ divider_color=“#eeeeee“]
Schritt 4: Multiplikation
Durch Multiplikation dieser Zahlen erhalten wir:
22 • 32 • 7 = 252
Auch hier machen wir wie in der ersten Aufgabe wieder eine Probe. Die Ergebnisse hieraus kannst du im nächsten Schritt verwenden, wenn wir die einzelnen Brüche auf den gemeinsamen Nenner erweitern.
252 : 7 = 36
252 : 2 = 126
252 : 3 = 84
252 : 4 = 63
252 : 9 = 28
Schritt 5: Brüche erweitern
Nun bringen wir alle Brüche auf denselben Nenner 252.
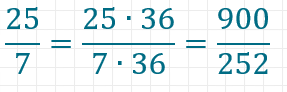
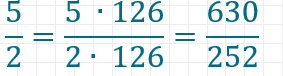
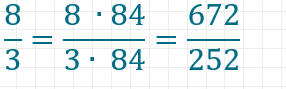
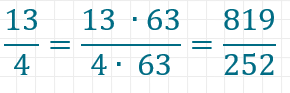
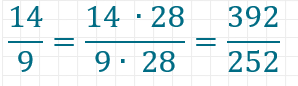
Schritt 6: Brüche vergleichen und sortieren
Nun können wir die einzelnen Brüche ganz einfach miteinander vergleichen, indem wir uns die unterschiedlichen Zähler anschauen. Es gilt also:
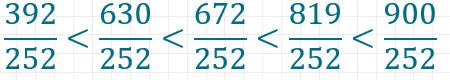
Damit die Aufgabe vollständig ist, schreiben wir als Ergebnis die ursprünglichen, nicht erweiterten Brüche aus der Aufgabenstellung in der entsprechenden Reihenfolge hin.