Viele Dinge verhalten sich in einem festen Verhältnis zueinander. Wie man diese Verhältnisse darstellen und damit rechnen kann, erfährst du in diesem Artikel.
Einfache Proportionalitäten
Proportionale Größen stehen immer im gleichen Verhältnis zueinander. Wird eine Größe vervielfacht, so wird auch die andere mit genau demselben Faktor vervielfacht.
An einem Beispiel ist das einfach zu erkennen: Stell dir vor, du sollst eine Wand streichen. Zum Test streichst du einen Quadratmeter Wand.
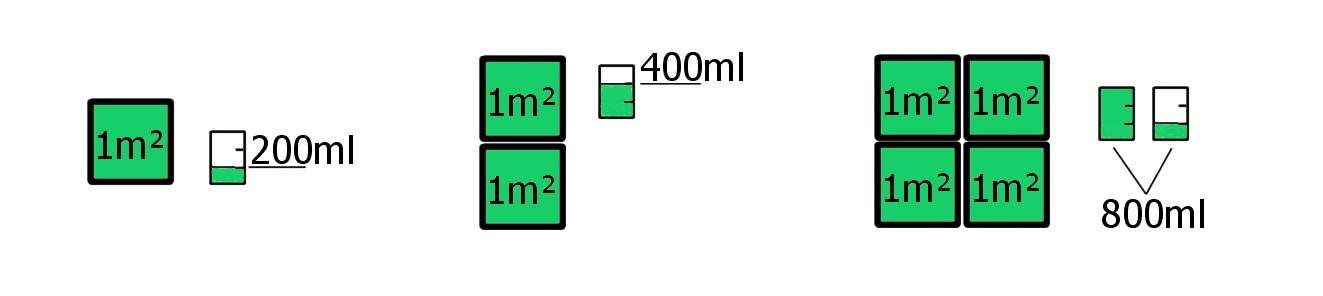
Wenn du 200 ml (0,2 Liter) Farbe benötigst, um einen Quadratmeter Wand zu streichen, wie viel Farbe wirst du dann wohl für zwei Quadratmeter benötigen? Natürlich genau doppelt so viel. Und für 4 Quadratmeter brauchst du vier mal so viel Farbe, wie für einen Quadratmeter. Wie kannst du diesen Zusammenhang mathematisch darstellen? Wenn du für die Farbe in ml die Variable y und für die Fläche der Wand in Quadratmetern die Variable x verwendest, dann gilt bei 200 ml Farbe pro Quadratmeter:
y = 200•x
Dabei nennt man die Zahl 200 den Proportionalitätsfaktor. Dieser Faktor beschreibt den Zusammenhang zwischen zwei Größen.
Wie viel Farbe würdest du für 50 Quadratmeter Wand brauchen?
y = 200•50
y = 10.000
Du würdest 10.000 ml, also 10 l Farbe brauchen.
[quads id=1]Würdest du nur 100 ml pro Quadratmeter brauchen, so wäre der Proportionalitätsfaktor 100 und du würdest für die 50 Quadratmeter nur 5 l Farbe benötigen.
Zwei Größen x und y, die durch solch einen Faktor in einem festen Verhältnis stehen (eine Größe ist m mal die andere Größe), nennt man proportional. Man schreibt „y ist proportional zu x“ als y ~ x.
Proportionale Funktionen
Exkurs Funktion
Eine Funktion ist schlicht ein mathematisches Konstrukt, das jedem Eingabewert einen Ausgabewert zuweist. Eine Funktion „Verdoppeln“ würde z.B. zu jedem Eingabewert den doppelten Ausgabewert liefern.
Definition
Proportionale Funktionen, die man auch als Proportionalitäten oder als homogene lineare Funktionen bezeichnet, sind Zuordnungen zwischen Argumenten x und Funktionswerten y der Form

Dabei ist m der konstante Proportionalitätsfaktor. Variablen, für die dieses Verhältnis m zusammengehöriger Werte (im obigen Beispiel z.B. 200 ml zu 1m² oder 1000 ml zu 5m²) immer konstant ist, heißen proportional.

TIPP: Manchmal findest du solche Funktionen auch umgeformt.
 lässt sich auch darstellen als:
lässt sich auch darstellen als:

Auch bei dieser Form handelt es sich um eine Proportionalität. Da sich dabei für m = 0 ein undefiniertes Ergebnis ergibt, darf m niemals 0 sein.
Vorbemerkung
Bei Graphen wird die vertikale Achse häufig als Ordinatenachse oder y-Achse bezeichnet, die horizontale Achse als Abszissenachse oder x-Achse.
Beispiel 1
Ein normales Auto verfügt über einen Motor. Zwei Autos haben also zwei Motoren, drei Autos drei Motoren usw. Wir können das einfach grafisch darstellen, indem wir auf der horizontalen Achse die Autos und auf der vertikalen die Motoren zählen.
[quads id=2]Bei einem Auto geht es auch eins nach oben, da es einen Motor gibt. Bei 2 Autos landet der Punkt schon zwei Einheiten weiter oben, da es auch zwei Motoren gibt. Verbinden wir alle Punkte mit einer Linie, erhalten wir folgende Grafik, wenn wir bis 10 Autos zählen.

Wenn y die Zahl der Motoren und a die Zahl der Autos ist, dann gilt offensichtlich y = a. Und was ist die Funktion für die durchgezogene Linie, auf der alle Werte liegen?
Eine Funktion, die uns in Abhängigkeit von der Zahl der Autos a einen Wert liefert, könnten wir als f(a) (gesprochen: f von a) bezeichnen.
In unserem Fall entspricht der Ausgabewert dem Eingangswert.
f(a) = a
Wenn du für die Darstellung von f(a) als Achse y wählst, kannst du auch einfach y = a schreiben.
Beispiel 2
Nehmen wir an, du sollst den Zusammenhang zwischen der Anzahl der Reifen und der Zahl der Autos berechnen. Wenn wir für jedes Auto 5 Reifen (Ersatzrad im Kofferraum) annehmen, dann kannst du das einfach so aufzeichnen:

Für jeden Schritt auf der horizontalen Achse müssen nun 5 Schritte auf der senkrechten Achse gemacht werden. Wie kannst du das als Formel darstellen?
Nennen wir die Zahl der Reifen r und die Zahl der Autos a. Dann ist r immer fünf mal so groß wie a. In der Funktionsschreibweise könntest du also eine Funktion r für die Reifenzahl schreiben: r(a) = 5a.
Umgekehrte oder indirekte Proportionalität
Ein Konzept mit vielen Namen. Der Zusammenhang wird auch als reziproke Proportionalität und als Antiproportionalität bezeichnet. Zwei Größen sind zueinander indirekt proportional, wenn sich eine davon proportional zum Kehrwert der anderen verhält.
Beispiel:


Wie du gut erkennen kannst, wird der Wert für y kleiner, je größer der Wert für x wird. Für den Betrag (der Betrag einer Zahl ist ihr Abstand von 0) gilt das auch auf der negativen Seite der Grafik. Eine solche Kurve ist typisch für antiproportionale Funktionen, man nennt sie eine Hyperbel.
Der Zusammenhang
 lässt sich umformen zu y • x = m.
lässt sich umformen zu y • x = m.
Zusammenhänge dieser Form wären z.B. die Seitenlängen einiger Figuren für gleiche Flächeninhalte.
Parallelogramm: Grundseite • Höhe = Fläche Rechteck: Länge • Breite = Fläche
Bei der Antiproportionalität ist also das Produkt zweier Größen immer konstant, man nennt das Produktgleichheit. Da das Produkt immer gleich bleibt, muss eine Größe kleiner werden, wenn die andere größer wird.
[quads id=3]Einfaches Beispiel Physik: Der Flug zum Mond
Du bist durch einen glücklichen Zufall an ein Raumschiff gekommen. Als ersten Ausflug planst du einen Trip zum Mond.
Doch wie lange dauert das eigentlich?
Der Mond ist etwa 400.000 km von der Erde entfernt. Bei einer mittleren Geschwindigkeit v(1) von 10.000km/h benötigst du also:

Stunden. Bei doppelter Geschwindigkeit brauchst du nur noch:

Stunden

Das Produkt aus Geschwindigkeit und Dauer ergibt immer die Entfernung. Geschwindigkeit und Dauer sind indirekt proportional zueinander.
Doppelte Geschwindigkeit bewirkt halbe Dauer. Doppelte Dauer bei halber Geschwindigkeit. Zehnfache Dauer bei einem Zehntel der Geschwindigkeit etc.
Beispiel Physik: Stromstärke
Das Ohmsche Gesetz U = R • I beschreibt den Zusammenhang zwischen Spannung U in Volt, Widerstand R in Ohm (dargestellt mit dem griechischen Omega) und Stromstärke I in Ampere.
In einem idealen Leiter ist der Widerstand normalerweise konstant. Betrachten wir einen Fall, in dem das nicht gilt und der Widerstand eines Stromkreises rapide kleiner wird.


Hier zeigt sich sofort die typische Struktur einer indirekten Proportionalität. Je kleiner der Widerstand, desto größer die Stromstärke. Für eine bestimmte Spannung kann man den Zusammenhang gut aufzeichnen.

Eine Glühbirne hat einen großen elektrischen Widerstand (etwa 100 Ohm). Wenn in dieser der Glühfaden „durchbrennt“, entsteht bei einer gasgefüllten Lampe häufig ein leitfähiges Plasma durch das ionisierte Material des Fadens. Dieses Plasma hat – im Gegensatz zu den 100 Ohm des intakten Fadens – fast keinen Widerstand mehr.
Wie du an der Grafik sehen kannst, nimmt die Stromstärke dann schwindelerregende Werte an: ein Kurzschluss. Einer von vielen guten Gründen, beim Umgang mit Elektrotechnik vorsichtig zu sein.
Und nun?
Proportionale Funktionen sind Sonderfälle von linearen Funktionen. Mit diesen einfachen mathematischen Werkzeugen lassen sich in Technik und Wirtschaft erstaunlich viele Zusammenhänge darstellen. Ganz besonders in der Physik wird dir ein Verständnis von Proportionalität sehr helfen.
