Primzahlen

Verwendete Zeichen und Vorbemerkung:

Das Multiplikationszeichen wird als Sternchen dargestellt *

Das Geteilt-Zeichen und der Bruchstrich finden sich im Text als /

Die Zahl 0 wird manchmal als natürliche Zahl definiert. In diesem Text wird 0 aber nicht zur Menge ℕ der natürlichen Zahlen gezählt.

Was sind Primzahlen?

Eine Primzahl ist eine natürliche Zahl (also eine der Zahlen {1,2,3,4,5,……}), die größer als 1 und nur durch sich selbst und die Zahl 1 teilbar ist. Das ist eine ziemlich einfache Regel. Doch für welche Zahlen gilt sie?

In steigender Größe angeordnet beginnt die Folge der Primzahlen so: (2,3,5,7,11,13,17,19,23,29,31,…). Eine Übersicht über alle Primzahlen bis 10.000 findest du hier.

Die Menge P der Primzahlen ist eine Teilmenge der natürlichen Zahlen ℕ und hat unendlich viele Elemente. Es gibt also keine größte Primzahl.

In der Einleitung hast du vielleicht schon bemerkt, dass fast alle natürlichen Zahlen sich als Produkt von Primzahlen darstellen lassen. So kann man die Zahl 6 auch als 2*3 schreiben oder die Zahl 125 als 5*5*5. Es gibt aber eine Ausnahme, denn die Zahl 1 ist keine Primzahl. Du kannst jede Zahl eindeutig als Produkt von Primfaktoren darstellen, doch mit der 1 als Primfaktor wäre das nicht mehr so: Statt 20 = 2*2*5 könntest du auch 20 = 1*2*2*5 schreiben. Als neutrales Element der Multiplikation verändert die 1 keine Zahl, mit der sie multipliziert wird, daher macht es keinen Sinn, sie als Faktor zu verwenden.

Primzahltests

Um herauszufinden, ob eine Zahl eine Primzahl ist, kannst du einen Primzahltest durchführen.

Methode 1: Probedivision

Wenn du eine natürliche Zahl n auf ihre Eigenschaft als Primzahl prüfen willst, kannst du nacheinander probieren, ob die Zahl durch eine Primzahl p teilbar ist. Dabei verwendest du Primzahlen steigender Größe. Wenn du keinen Prim-Teiler findest, dann ist n eine Primzahl.

Ist die Zahl 19 eine Primzahl?

19 ist nicht durch 2 teilbar

19 ist nicht durch 3,5,7,11,13,17 teilbar

Also ist die Zahl 19 eine Primzahl.

Doch halt: Musst du wirklich alle Primzahlen kleiner als n prüfen?

Nein! Denn die kleinste Primzahl, die als Teiler infrage kommt, ist die Zahl 2, die größte ist die Wurzel aus n.

Warum das?

Wenn eine Zahl n zwei Faktoren (a,b) hat und ein Faktor größer oder gleich der Wurzel aus der Zahl und der andere Faktor größer als die Wurzel aus der Zahl ist, dann wäre das Produkt größer als die Zahl.

Es kann höchstens ein Faktor größer als die Wurzel aus der zu prüfenden Zahl sein, der andere Faktor muss kleiner sein. Wenn du also der Größe nach alle Faktoren prüfst, die kleiner als diese Wurzel sind, würde ein größerer Faktor übrig bleiben, falls es einen gibt.

Zurück zu unserem Beispiel:

Ist die Zahl 19 eine Primzahl?

Quadratwurzel von 19: Gerundet 4,36

Wir prüfen also Teiler kleiner als 4,36, die Primzahlen sind.

19 ist nicht durch 2 teilbar.

19 ist nicht durch 3 teilbar.

Gäbe es einen Primfaktor größer als 4,36, so müsste der andere Primfaktor kleiner sein, damit das Produkt der Primfaktoren nicht größer als 19 wird. Da wir keinen kleineren Primfaktor gefunden haben, kann es auch keinen größeren geben, der mit diesem multipliziert 19 ergibt.

Methode 2: Das Sieb des Eratosthenes

Dieses Verfahren zum Suchen nach Primzahlen ist schon lange bekannt, die Bezeichnung als Sieb geht auf den griechischen Mathematiker Eratosthenes zurück.

Wenn du selbst Primzahlen aussieben möchtest, schreibst du zunächst der Reihe nach natürliche Zahlen auf. Dabei beginnst du nach der Zahl 10 (und dann nach 20, 30…) eine neue Reihe und machst weiter, bis du die größte Zahl erreicht hast, die du prüfen möchtest. Sobald du mit der Probedivision eine Zahl als Primzahl bestimmt hast, streichst du alle Vielfachen dieser Zahl durch oder markierst sie farbig, denn es sind keine Primzahlen. Du musst nur Vielfache von Primzahlen streichen, wenn die Primzahlen kleiner als die Quadratwurzel der größten zu prüfenden Zahl sind.

Hier wurde 110 als größte zu prüfende Zahl gewählt. Die Quadratwurzel von 110 ist etwa 10,49. Wir markieren alle Vielfachen von Primzahlen p für die gilt: p ist kleiner als 10,49. Wir beginnen mit der kleinsten Primzahl 2 und markieren deren Vielfache.

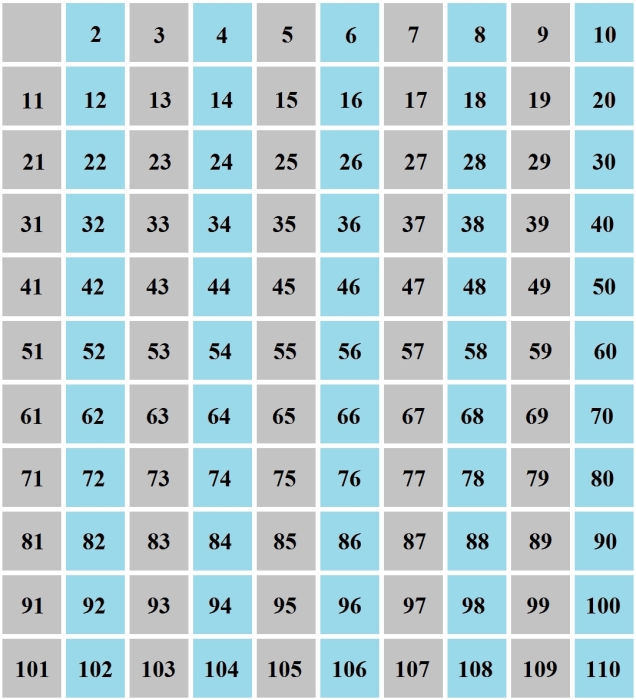
Nun fügen wir die Vielfachen der Primzahlen 3,5 und 7 hinzu.

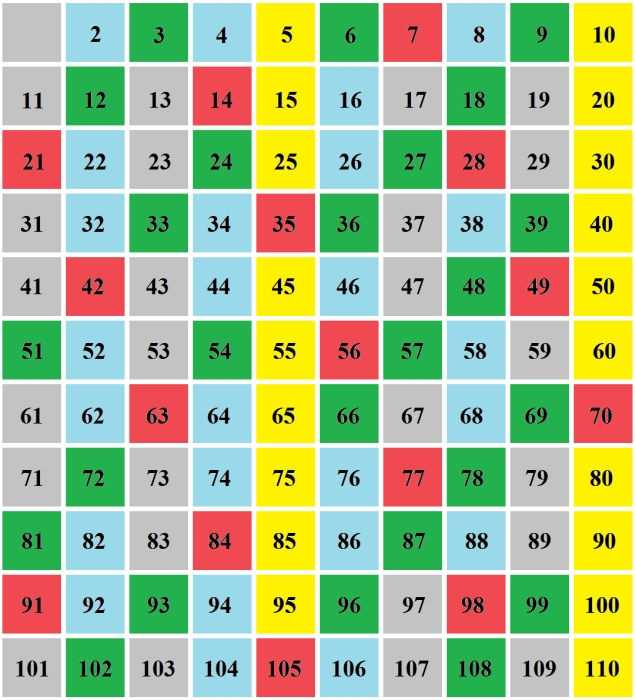
Alle nun nicht markierten Zahlen sind Primzahlen. Wir haben bereits die Primzahlen 2,3,5 und 7 markiert. Zu diesen kommen die nun gefundenen Primzahlen: 11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109

Warum sind Primzahlen wichtig?

Anwendung in der Mathematik

Im Mathematikunterricht gibt es einige Anwendungen für Primzahlen, doch besonders im Bereich des Bruchrechnens werden sie häufig verwendet.

Wenn du einen Bruch kürzen sollst, kannst du mittels des ggT (größter gemeinsamer Teiler) die Zahl ermitteln, durch die du Zähler und Nenner teilen musst, um den Bruch in maximal gekürzter Form zu erhalten. Der ggT zweier Zahlen kann ermittelt werden, indem alle Primfaktoren, die sowohl in der Zerlegung der ersten Zahl, als auch in der Zerlegung der zweiten Zahl vorkommen, in ihrer kürzesten Kette multipliziert werden.

Gilt es, einen gemeinsamen Nenner für die Addition oder Subtraktion zweier Brüche zu finden, dann sollte dieser Nenner so klein wie möglich sein, damit du nicht mit unnötig großen Zahlen rechnen musst. Das kgV (kleinste gemeinsame Vielfache) der beiden Nenner ergibt diesen kleinsten Nenner. Um das kgV zweier Zahlen zu ermitteln, werden alle (in mindestens einer der Zahlen) vorkommenden Primfaktoren in ihrer längsten Kette multipliziert.

Primzahlen in der Praxis

Außerhalb des Mathematikunterrichts sind Primzahlen in der Informatik extrem wichtig. Die Tatsache, dass zwei Primzahlen einfach miteinander multipliziert werden können, aber es sehr schwierig ist, aus dem Produkt wieder die Primfaktoren zu ermitteln, ist die Grundlage für fast alle Verschlüsselungsverfahren im Internet. Ganz gleich, ob du jemandem eine Textnachricht schreibst oder online eine Überweisung auf ein Konto ausfüllst, deine Daten sollen geheim bleiben. Ohne Primzahlen keine moderne Kryptographie (die Lehre der Verschlüsselung, vom Altgriechischen kryptos: verborgen) und ohne Kryptographie wären weder sichere Funkschlüssel noch der geschützte Betrieb von Fahrzeugelektronik oder Onlineshops möglich.