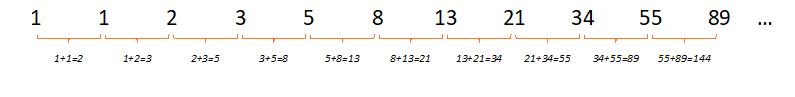Was sind die Fibonacci-Zahlen?
Die Fibonacci-Folge beginnt mit zwei Einsen. Jedes weitere Glied der Folge ist die Summe der beiden vorhergehenden Glieder. Das Ganze sieht also wie folgt aus:
Du kannst die Ermittlung der Zahlen der Folge auch als Formel schreiben:
an = an-1 + an-2, mit a1, a2 = 1
[quads id=1]
Eigenschaften der Fibonacci-Zahlen
Die Fibonacci-Zahlen sind durch verschiedene Eigenschaften gekennzeichnet. Zunächst einmal handelt es sich bei der Zahlenfolge um eine Reihe natürlicher Zahlen. Da die Summe zweier natürlicher Zahlen immer auch eine natürliche Zahl ist, ist klar, dass alle Zahlen in der Fibonacci-Folge natürliche Zahlen sind. Außerdem ist die Reihe unendlich. Sie hat zwar einen festgelegten Anfang (1, 1), aber anschließend kannst du immer weiter die Summe der beiden Vorgänger-Zahlen bilden. Das Verhältnis zweier aufeinanderfolgender Zahlen der Fibonacci-Reihe nähert sich dem Goldenen Schnitt an. Als Goldenen Schnitt bezeichnet man die Einteilung einer Strecke in der Weise, dass das Verhältnis der Gesamtstrecke zum größeren Teil dem Verhältnis des größeren Teils zum kleineren entspricht. Dem goldenen Schnitt wird eine besondere ästhetische Wirkung zugeschrieben. Daneben findet man ihn auch in der Natur immer wieder vor. Je weiter du in der Fibonacci-Folge voranschreitest, desto näher kommt das Verhältnis zweier aufeinanderfolgender Zahlen dem Goldenen Schnitt, und zwar abwechselnd aus beiden “Richtungen”. Ein Quotient ist größer als der goldene Schnitt, der nächste kleiner. Übrigens sind zwei aufeinander folgende Fibonacci-Zahlen immer teilerfremd, das heißt, ihr größter gemeinsame Teiler ist immer die 1.Die Entdeckung der Fibonacci-Reihe
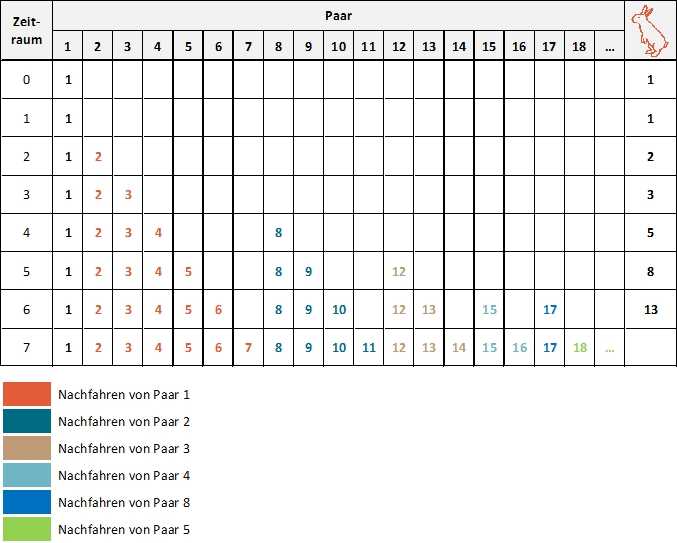
Wie kommt man auf die Idee, eine solche Zahlenfolge zu entwickeln? Der Forscher Fibonacci (eigentlich Leonardo da Pisa) untersuchte das Wachstum von Kaninchenpopulationen. Die Idee dahinter ist folgende: Mit einem einzigen Kaninchen-Paar kann man eine gesamte Kaninchenpopulation aufbauen, und zwar ziemlich schnell. Zu Beginn lebt genau ein Paar Kaninchen. Da die Fortpflanzung Zeit braucht, bleibt das Paar im ersten betrachteten Zeitraum noch alleine. Ab dem nächsten Zeitraum kommt jedoch in jedem Zeitraum ein weiteres Paar hinzu – die Nachfahren von Paar 1. Auch die Nachfahren von Paar 1 zeugen weitere Nachfahren, jeweils immer, nachdem sie einen Zeitraum lang gewartet haben. Wenn alle Kaninchenpaare ewig überleben, erhält man die Fibonacci-Folge als Ergebnis. Die folgende Tabelle zeigt dies noch einmal deutlicher:
Fibonacci war jedoch nicht der erste, der die nach ihm benannte Folge entdeckte. Die Reihe wurde auch vorher schon genutzt, um Wachstum in der Natur zu beschreiben.
[quads id=2]
Wo kommen die Fibonacci-Zahlen vor?
Wenn man Linien von der Länge der Fibonacci-Zahlen anordnet, erhält man eine Spirale. Solche Spiralen finden sich in der Natur recht häufig, beispielsweise in Blättern oder in Bäumen. Außerdem finden Fibonacci-Zahlen in der Finanzmathematik Anwendung, um die Entwicklung von Aktienkursen zu beschreiben. Die Projektmanagementmethode Scrum verwendet ebenfalls (angepasste) Fibonacci-Zahlen, um die Komplexität von Aufgaben einzuschätzen. 1 ist dabei nicht sehr komplex, 2 schon etwas komplexer. Der Abstand an Komplexität erhöht sich immer weiter, weil auch die Unsicherheit wächst. [quads id=3] Auch im Pascalschen Dreieck kannst du die Fibonacci-Folge finden.Wie hilfreich war dieser Beitrag?
Klicke auf die Sterne um zu bewerten!