Wenn du in der Schule Wahrscheinlichkeitsrechnung und die Berechnung statistischer Kennwerte lernst, wirst du sicher auch bald über Boxplots stolpern. Wir erklären dir, worum es sich dabei handelt und wie du selbst Boxplots erstellst.
Was sind Boxplots und wozu braucht man sie?
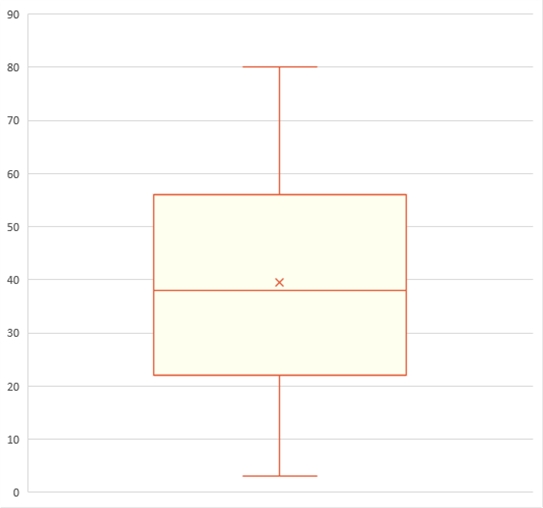
Boxplots sind eine ganz bestimmte Art von Graphik, mit der eine Verteilung visualisiert wird. Der Name setzt sich zusammen aus Box = Kasten und plot = zeichnen. Boxplots sehen wie folgt aus:
Welche Informationen werden in Boxplots dargestellt?
Um Boxplots zu verstehen, musst du ein bisschen über statistische Kennwerte wissen, daher folgt hier eine kurze Wiederholung. Uwe hat eine große Familie mit vielen Cousins, Cousinen, Tanten und Onkeln. Er möchte eine Statistik dazu erstellen, wie alt seine Verwandten sind. Dazu stellt er die folgende Liste auf.
| Name | Alter |
| Uwe | 16 |
| Marie | 12 |
| Gert | 45 |
| Greta | 38 |
| Georg | 65 |
| Anna-Lena | 3 |
| Mareike | 19 |
| Marcel | 26 |
| Elisabeth | 78 |
| Wilhelm | 79 |
| Johannes | 42 |
| Tina | 40 |
| Sibylle | 48 |
| Andreas | 32 |
| Luisa | 14 |
| Sebastian | 25 |
| Svenja | 40 |
| Friedrich | 64 |
| Kerstin | 35 |
| Klara | 80 |
| Margarete | 30 |
Da die Liste nicht sehr übersichtlich ist, erstellt er die folgende Graphik.
Häufigkeitsverteilung aufstellen
So richtig aussagekräftig ist das aber noch nicht. Auf den ersten Blick hat Uwe das Gefühl, dass seine Familienmitglieder meistens über 40 sind. Um das zu prüfen, erstellt er eine Häufigkeitsverteilung, das heißt, er zählt für jedes Alter aus, wie viele Familienmitglieder genau so alt sind. Als Ergebnis erhält er die folgende Grafik:
| Alter | Anzahl |
| 3 | 1 |
| 12 | 1 |
| 14 | 1 |
| 16 | 1 |
| 19 | 1 |
| 25 | 1 |
| 26 | 1 |
| 30 | 1 |
| 32 | 1 |
| 35 | 1 |
| 38 | 1 |
| 40 | 2 |
| 42 | 1 |
| 45 | 1 |
| 48 | 1 |
| 64 | 1 |
| 65 | 1 |
| 78 | 1 |
| 79 | 1 |
| 80 | 1 |
Er erstellt ein neues Diagramm, das schon ein paar Informationen mehr bereithält.
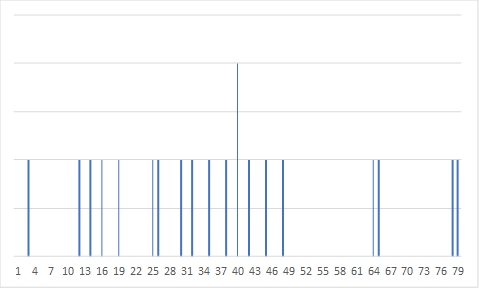
Offensichtlich sind die Familienmitglieder doch jünger, als Uwe auf den ersten Blick dachte. Das Diagramm ist ihm jedoch zu unübersichtlich. Uwe erinnert sich an den Statistik-Unterricht und rechnet ein paar statistische Kennwerte aus.
[quads id=2]Statistische Kennwerte errechnen
Arithmetisches Mittel
Am einfachsten ist das arithmetische Mittel, weil er das aus der Berechnung des Notendurchschnitts kennt. Um das arithmetische Mittel zu berechnen, muss man nur alle einzelnen Werte addieren und durch die Anzahl der Werte teilen.
Uwe rechnet also: (16+12+45+38+65+3+19+26+78+79+42+40+48+32+14+25+40+64+35+80+30):21=831:21=39,57
Uwes Familienmitglieder sind also im Durchschnitt 39,57 Jahre alt.
Median
Cousine Anna-Lena ist mit 3 Jahren noch sehr jung, und Uwe weiß, dass solche “Ausreißer” in den Daten das Bild gerade beim arithmetischen Mittel verfälschen können. Daher berechnet er zusätzlich den Median. Der Median ist der mittlere Wert der Verteilung. Um ihn zu finden, muss Uwe alle Daten der Größe nach sortieren und dann den Wert wählen, der genau in der Mitte steht.
Welcher Platz das ist, kannst du herausfinden, indem du von der Gesamtzahl 1 abziehst, diese Zahl durch 2 teilst und dann wieder 1 addierst, also (21-1):2 + 1 = 20:2 + 1 = 10 + 1 = 11. Bei 21 Werten ist dies der elfte Platz. Uwe sortiert und zählt und erhält 38 als Median. Hätte er nur 20 Familienmitglieder, gäbe es keinen mittleren Wert. In diesem Fall müsste er das arithmetische Mittel aus dem 10. und 11. Platz bilden.
Quartile
Ähnlich wie der Median funktionieren auch Quartile. Sie teilen die Verteilung nicht in zwei gleiche Teile, sondern in 4, und geben an, welcher Wert an diesen Grenzen steht. Genau genommen ist der Median ein Quartil, und zwar das zweite. Das erste Quartil gibt an, welcher Wert größer als ein Viertel aller Werte und kleiner als drei Viertel aller Werte ist, beim dritten Quartil ist es umgekehrt.
Die Berechnung der Plätze, die Uwe auszählen muss, erfolgt genauso wie beim Median, nur, dass du nicht durch 2, sondern durch 4 teilst, also (21 – 1) : 4 + 1 = 20 : 4 + 1 = 5 + 1 = 6 für das erste Quartil und 16 für das dritte Quartil. Uwe rechnet beide Quartile aus und erhält 25 für das erste und 48 für das dritte Quartil.
[quads id=3]Boxplot zeichnen
Mit diesen Informationen kann er nun ein Boxplot-Diagramm zeichnen. Dort werden für eine Verteilung nämlich beide Quartile und der Median abgebildet. Das erste (untere) Quartil bildet den Boden des Kastens, das dritte (obere) Quartil die Decke. Dazwischen wird auf Höhe des Medians eine Linie eingezeichnet. Das arithmetische Mittel wird als Kreuz eingezeichnet. Man kann außerdem durch Linien das Minimum und das Maximum der Verteilung angeben. Uwe möchte das auch tun. Das Minimum ist 3 und das Maximum 80. Also zeichnet er:
Anhand dieser Graphik kann man erkennen, dass die meisten Familienmitglieder zwischen 25 und 48 Jahre alt sind und im Mittel knapp unter 40. Diese Informationen kannst du aus Boxplots auch ablesen, ohne dass du die zugrundeliegende Verteilung kennst.
Wie hilfreich war dieser Beitrag?
Klicke auf die Sterne um zu bewerten!