Im Mathematik-Unterricht spielt die Geometrie immer wieder eine große Rolle. Dort befasst du dich mit geometrischen Figuren und ihren jeweiligen Eigenschaften. In diesem Artikel geben wir dir einen Überblick über die verschiedenen Figuren und erklären dir, wozu du dich mit diesem Thema überhaupt beschäftigen musst.
Was sind geometrische Figuren?
Eine exakte Definition, was geometrische Figuren eigentlich sind, gibt es nicht. Sie teilen jedoch einige Eigenschaften:
- Du kannst sie anhand bestimmter Merkmale in die unten stehenden Kategorien einordnen.
- Du kannst sie zeichnen und bestimmte Eigenschaften messen oder berechnen.
- Sie sind Abstraktionen von Figuren, die man auch in der Natur findet, und helfen so dabei, unsere Umgebung wissenschaftlich zu untersuchen.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=1]
[su_divider top=“no“ divider_color=“#eeeeee“]
Im Mathe-Unterricht beschäftigst du dich die meiste Zeit mit geometrischen Figuren im zweidimensionalen Raum, also in der Ebene. Es gibt aber auch geometrische Figuren im dreidimensionalen Raum, die man Körper nennt. Diese haben meist eine Entsprechung im zweidimensionalen Raum (zum Beispiel verhält sich die Kugel so ähnlich wie ein Kreis). In diesem Artikel gehen wir nur auf geometrische Figuren in der Ebene ein.
Wozu untersucht man in der Mathematik geometrische Figuren?
Wie oben bereits geschrieben sind geometrische Figuren Abstraktionen der realen Welt. Wenn du also Wissen über Dreiecke oder Kreise hast, kannst du dieses anwenden, um entsprechende Figuren in der Natur zu untersuchen. Ein besonders bekanntes Beispiel ist der Satz des Pythagoras, der in rechtwinkligen Dreiecken angewendet werden kann. Du kannst ihn nutzen, um die Entfernung zwischen zwei Punkten zu bestimmen.
Dies gilt auch für alle anderen geometrischen Figuren: Immer gibt es Anwendungen in den Naturwissenschaften oder in den Geisteswissenschaften, die durch die Berechnungen in Figuren Aussagen über Zusammenhänge treffen können.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=2]
[su_divider top=“no“ divider_color=“#eeeeee“]
Welche geometrischen Figuren gibt es?
Punkte
Ein Punkt ist die einfachste geometrische Figur. Er hat weder eine Länge noch eine Breite und ist ausschließlich durch seine Lage im Koordinatensystem bestimmt. Die Lage des Punkts wird dabei in der folgenden Form angegeben: Bezeichnung des Punkts (Lage auf der x-Achse | Lage auf der y-Achse). Im Beispiel unten wäre das also A(1|3).

Geraden, Halb-Geraden und Strecken
Eine Gerade verläuft immer durch zwei Punkte. Durch zwei beliebige Punkte auf einer Gerade kann man diese also exakt bestimmen, denn es gibt immer nur eine Gerade, die durch genau diese beiden Punkte verläuft. Eine Gerade ist unendlich, hat also weder einen Anfang noch ein Ende. Das folgende Bild zeigt ein Beispiel für eine Gerade, die durch die Punkte A(1|3) und A(3|2) verläuft.

Eine Halbgerade besitzt einen Anfang (oder ein Ende), ist aber auf der anderen Seite unendlich. Sie wird also definiert durch den Anfangspunkt und einen weiteren Punkt, durch den sie verläuft. Die Grafik zeigt eine Halbgerade, die im Punkt A(1|3) beginnt und durch den Punkt A(3|2) verläuft. Eine Halbgerade wird auch als Strahl bezeichnet.

Daneben gibt es außerdem Strecken, die einen Anfang und ein Ende, und somit auch eine klar definierte Länge besitzen. Im folgenden ist die Strecke abgebildet, die die Punkte A(1|3) und A(3|2) miteinander verbindet.

Polygone
Polygone verbinden drei oder mehr Punkte zu einer Form. Ein Polygon hat immer so viele Seiten wie Punkte und Winkel. Sie werden mit der Anzahl der Punkte als Drei-, Vier-, Fünf- oder einfach Vielecke bezeichnet.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=3]
[su_divider top=“no“ divider_color=“#eeeeee“]
Dreiecke
Dreiecke besitzen drei Punkte und somit auch drei Seiten. Die Summe aller Winkel im Dreieck ergibt immer exakt 180°. Wenn du also zwei Winkel kennst, kannst du ganz einfach die anderen beiden ausrechnen. Daneben gibt es Dreiecke mit besonderen Formen, für die man einfacher Berechnungen vornehmen kann. Dies sind:
- das gleichseitige Dreieck (alle drei Seiten sind gleich lang),
- das gleichschenklige Dreieck (zwei der drei Seiten sind gleich lang),
- das rechtwinklige Dreick (einer der drei Winkel ist exakt 90° groß).
Die folgende Abbildung zeigt ein ungleichmäßiges Dreieck, auf das keine Besonderheiten zutreffen.
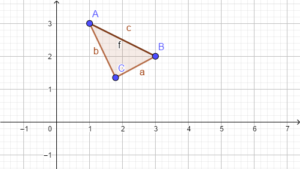
Vierecke
Vierecke sind ebenfalls sehr häufig und du wirst in der Schule sehr viel über sie lernen. Vier Punkte werden durch vier Seiten miteinander verbunden. Die Summe der Winkel in einem Viereck ergibt immer genau 360°. Folgende „besondere“ Vierecke kennt die Mathematik:
- das Quadrat (alle vier Seiten sind gleich lang, dadurch sind alle Winkel 90° groß),
- das Rechteck (die jeweils gegenüberliegenden Seiten sind gleich lang und alle WInkel sind 90° groß),
- das Trapez (zwei Seiten des Vierecks sind parallel zueinander),
- die Raute (alle vier Seiten sind gleich lang),
- das Parallelogramm (die jeweils gegenüberliegenden Seiten sind gleich lang und parallel zueinander).
Das folgende Viereck ist ein ungleichmäßiges Viereck ohne besondere Eigenschaften.
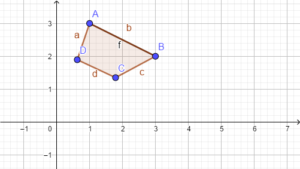
Andere Polygone
Andere Polygone werden im Mathe-Unterricht kaum untersucht, aber natürlich kannst du sie mit beliebig vielen Punkten und Seiten zeichnen.
Kreise
Ein Kreis ist eine geometrische Figur, in der jeder Punkt denselben Abstand zum Mittelpunkt der Figur hat. Ein Kreis wird daher bestimmt durch seinen MIttelpunkt und den Radius, also den Abstand zwischen Mittelpunkt und Kreislinie.

