Die Art, wie wir Zahlen schreiben, geht uns irgendwann so in Fleisch und Blut über, dass wir sie für die einzig mögliche halten. Dabei ist das Dezimalsystem mit arabischen Ziffern, das wir verwenden, zwar sehr gebräuchlich, aber es gibt noch viele weitere Möglichkeiten, den Wert einer Zahl aufzuschreiben. In der Schule lernt man daher auch andere Stellenwertsysteme kennen und außerdem Römische Zahlen. Was ein Stellenwertsystem ist und wie du eine Zahl von einem in ein anderes überträgst, erfährst du in diesem Artikel.
Was sind Stellenwertsysteme?
Als Stellenwertsystem bezeichnet man eine Möglichkeit, wie man den Wert einer Zahl darstellen kann. Grundsätzlich werden Zahlen immer mit verschiedenen unterschiedlichen Zeichen geschrieben. Diese Zeichen besitzen einen bestimmten Wert. Bei einem Stellenwertsystem ändert sich dieser Wert abhängig von der Stelle an der das Zeichen steht – daher der Name. Unser Dezimalsystem ist ein solches Stellenwertsystem. Die Ziffer 1 hat den Wert 1, wenn sie an der letzten Stelle steht, den Wert 10, wenn sie an zweitletzter Stelle steht, 100 an drittletzter Stelle und so weiter.
Alle Stellenwertsysteme funktionen also nach folgendem Prinzip: Man nimmt eine bestimmte Anzahl von verschiedenen Zeichen. Im Dezimalsystem sind das die zehn Ziffern. Diese bringt man in eine Reihenfolge, in der ein Zeichen immer genau um den Wert 1 größer ist als das vorangegangene, also 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Wenn man alle Zeichen „verbraucht“ hat, schreibt man den nächsthöheren Wert, indem man die zweite Stelle (von hinten) belegt und dort mit dem nächsten Zeichen anfängt, also 10. Dann lässt man die Zeichen an der letzten Stelle wieder „durchlaufen“ und zählt anschließend die vorletzte Stelle hoch.
[su_divider top=“no“ divider_color=“#eeeeee“]
[su_divider top=“no“ divider_color=“#eeeeee“]
Ein ungewöhnliches Stellenwertsystem
Das funktioniert mit Ziffern, aber auch mit anderen Symbolen. Wir könnten uns beispielsweise ein eigenes Stellenwertsystem ausdenken, das die Symbole ♥, → und ✁ enthält, also genau drei verschiedene Symbole. Damit können wir unser eigenes Zahlensystem aufbauen. Wir ordnen dem Herz den Wert 0, dem Pfeil den Wert 1 und der Schere den Wert 2 zu. Die folgende Tabelle zeigt, wie leicht man in einem solchen System „hochzählen“ und jeden Wert erhalten kann. 15 würde man in diesem System also schreiben: →✁♥
| Zahl | Wert |
| ♥ | 0 |
| → | 1 |
| ✁ | 2 |
| →♥ | 3 |
| →→ | 4 |
| →✁ | 5 |
| ✁♥ | 6 |
| ✁→ | 7 |
| ✁✁ | 8 |
| →♥♥ | 9 |
| →♥→ | 10 |
| →♥✁ | 11 |
| →→♥ | 12 |
| →→→ | 13 |
| →→✁ | 14 |
| →✁♥ | 15 |
Du siehst, man kann mit jeglichen Symbolen in einem Stellenwertsystem alle anderen Zahlen darstellen. Meist verwendet man als Symbole jedoch die Ziffern oder – wenn es mehr als 10 verschiedene Zeichen sein sollen – zusätzlich Buchstaben, die man einfach in der Reihenfolge ihres Vorkommens im Alphabet sortiert. Um nicht jedes Mal sagen zu müssen, welche Symbole man für ein Stellenwertsystem verwendet, gibt man einfach die Basis an. Basis 10 bedeutet, dass man 10 Zeichen (also die Ziffern) verwendet und bezeichnet daher unser Dezimalsystem. Basis 20 würde bedeuten, dass außer den zehn Ziffern noch die zehn ersten Buchstaben des Alphabets, also A, B, C, D, E, F, G, H, I, J verwendet werden.
Andere Arten, Zahlen zu schreiben
Außer Stellenwertsystemen gibt es übrigens auch noch Additionssysteme. Die römischen Zahlen sind ein solches Additionssystem. Hier hat jedes Symbol einen Wert, der unabhängig von der Stelle ist. Der Gesamtwert der Zahl wird durch Addition (oder auch Subtraktion) der einzelnen Symbole ermittelt. Im direkten Vergleich stellt sich auch der große Vorteil von Stellenwertsystemen heraus: Sie sind sehr einfach und man kann mit sehr wenigen verschiedenen Symbolen beliebig große Zahlen darstellen. Bei Additionssystemen braucht man für immer größere Zahlen auch neue Zeichen, sodass man römische Zahlen beispielsweise nur bis zum Wert 3 999 darstellen kann. Stellenwertsysteme kennen dieses Problem nicht.
[su_divider top=“no“ divider_color=“#eeeeee“]
[su_divider top=“no“ divider_color=“#eeeeee“]
Wozu braucht man andere Stellenwertsysteme?
Die beiden bekanntesten Stellenwertsysteme außer dem Dezimalsystem, mit denen du täglich zu tun hast (auch, wenn es dir vielleicht nicht bewusst ist), sind das Dual- und das Hexadezimalsystem. Das Dualsystem besteht nur aus Einsen und Nullen. Es wird vor allem in der Digitaltechnik verwendet, und alle Computer benötigen es. Der Vorteil am Dualsystem ist, dass man eigentlich gar keine Symbole braucht. Man muss nur für jede Stelle einer Zahl wissen, ob dort eine eins steht oder nicht. Man kann daher Zahlen auch leicht über elektrischen Strom darstellen, indem man für die 1 den Zustand „Strom fließt“, also „an“, verwendet, und für die 0 „Strom fließt nicht“, also „aus“. Um eine beliebig große Zahl darzustellen, muss man einem Computer also gar keine verschiedenen Symbole übermitteln, sondern nur den Unterschied zwischen „an“ und „aus“.
Auch das Hexadezimalsystem wird in der Informatik verwendet, weil es sich leichter speichern und darstellen lässt als das Dezimalsystem. Da gerade in den Anfängen der Datenverarbeitung sehr wichtig war, wieviel Speicherplatz man für bestimmte Informationen verbrauchte, setzte sich hier auch schnell das Hexadezimalsystem mit den zehn Ziffern und den Buchstaben A, B, C, D, E, F durch. Vielleicht hast du schon einmal gesehen, wie ein Farbcode dargestellt wird. Hierzu sind verschiedene Schreibweisen möglich, darunter auch die Notation als Hexadezimalzahl.
Umrechnen von einem System ins andere
Die meisten Schülerinnen und Schüler tun sich anfangs mit dem Erlernen und Berechnen von Zahlen in anderen Stellenwertsystemen schwer. Das liegt natürlich einerseits an der Gewöhnung an das Dezimalsystem. Andererseits wirkt jedes Stellenwertsystem auf uns „unnatürlich“, weil sich die Namen der Zahlen, wie wir sie kennen, aus dem Dezimalsystem ableiten. Eine 25 behält im Namen zum Beispiel immer noch die Information, dass an der ersten Stelle eine 2 („zwanzig“) und an der zweiten eine 5 („fünfund…“) steht, auch wenn sie im Dezimalsystem 11001 geschrieben wird. Zwar wäre die korrekte Aussprache eigentlich nun eine andere, aber unser Zahlengefühl funktioniert eben bei einer 25 besser als bei einer 11001 im Dualsystem.
Die Umrechnung vom einen ins andere System ist jedoch ganz einfach. Dabei kommt es natürlich darauf an, von welchem in welches System du umrechnen möchtest. Das Dezimalsystem solltest du dabei notfalls immer als Zwischenschritt verwenden, sodass es für dich reicht, die beiden folgenden Methoden zu kennen.
[su_divider top=“no“ divider_color=“#eeeeee“]
[su_divider top=“no“ divider_color=“#eeeeee“]
Umrechnen einer Zahl ins Dezimalsystem
Um eine beliebige Zahl aus einam anderen Stellenwertsystem ins Dezimalsystem umzurechnen, musst du nur die Zahl selbst und die Basis des Stellenwertsystems wissen. Nun gehst du Stelle für Stelle von hinten nach vorne durch und multiplizierst jeden Wert mit der Basis potenziert mit der Stelle -1. Das hört sich komplizierter an, als es ist, daher folgt hier ein konkretes Beispiel.
Aufgabe: Stelle die Zahl (32012)4 im Dezimalsystem dar.
| |
|
| |
|
(32012)4 ist also gleich mit 902 im Dezimalsystem.
Umrechnen einer Zahl aus dem Dezimalsystem
Natürlich kannst du auch eine Zahl aus dem Dezimalsystem in jedes beliebige andere Zahlensystem umrechnen. Die Vorgehensweise ist ein bisschen anders, aber genauso leicht. Du musst nur die Zahl durch die gewünschte Basis teilen und dir den Rest notieren. Dieser Rest ist die letzte Stelle deiner neuen Zahl. Das Ergebnis teilst du nun wieder durch die Basis. Der Rest ist die zweitletzte Stelle. Du setzt das ganze so lange fort, bis das Ergebnis 0 ist. Um es leichter zu verstehen, rechnen wir einfach das Beispiel von oben einmal in umgekehrter Richtung.
Aufgabe: Stelle die Zahl 904 in einem Stellenwertsystem zur Basis 4 dar.
904 : 4 = 225, Rest 2
225 : 4 =56, Rest 1
56 : 4 = 14, Rest 0
14 : 4 = 3, Rest 2
3 : 4 = 0, Rest 3
902 ist also gleich mit (32012)4.
[wp-svg-icons icon=“warning“ wrap=“i“] Wichtig: Der Rest, den du als erstes ermittelst, ist die letzte Stelle der Zahl, nicht umgekehrt.
Wie du die unbekannte Basis eines Stellenwertsystems bestimmen kannst
Eine weitere mögliche Aufgabenstellung zu Stellenwertsystemen besteht darin, die unbekannte Basis eines Stellenwerts zu bestimmen, wenn du nur die Zahl im Dezimalsystem und die im zu bestimmenden Stellenwertsystem kennst. Hierzu benötigst du wieder die Vorgehensweise, die du auch nutzt, um eine Zahl ins Dezimalsystem zu überführen. Da du die Basis aber noch nicht kennst, musst du eine Gleichung mit einer Variablen erstellen, die du entsprechend lösen musst. Auch dies erklären wir wieder anhand eines Beispiels:
Aufgabe: Ermittle die Basis x eines Stellenwertsystems für das gilt 520x = 259.
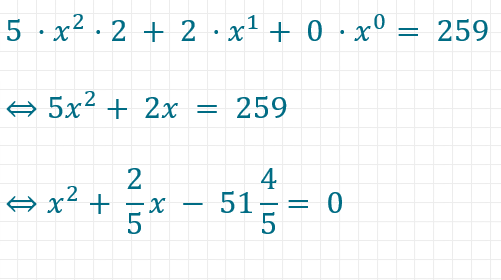
Mit Hilfe der p-q-Formel lässt sich diese Gleichung dann wie folgt auflösen.
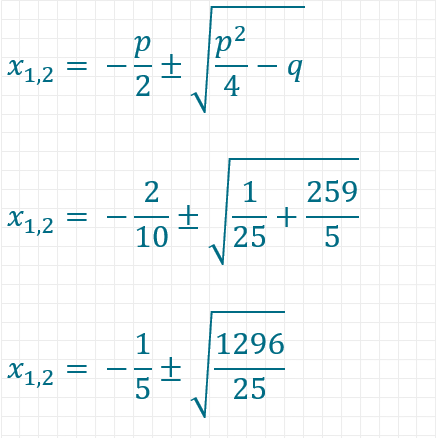
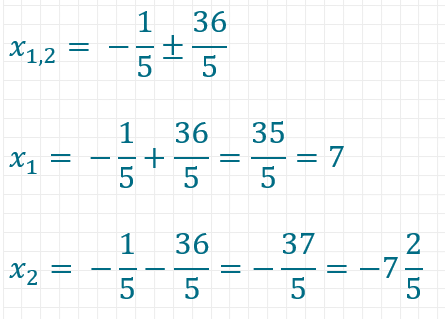
Da die Basis für ein Stellenwertsystem positiv sein muss, beträgt sie in diesem Fall 7.
Wir hoffen, dass diese Erklärung dir geholfen hat.
