Das Skalenniveau oder Messniveau bestimmt, auf welche Weise du ein Merkmal messen kannst. Dies ist wichtig, weil du daraus ableiten kannst, welche weiteren statistischen Berechnungen du mit diesen Daten vornehmen kannst. Wir erklären dir in diesem Artikel, was das Skalenniveau ist und welche Bedeutung es in der Statistik hat.
Merkmale und Skalenniveaus
Als Merkmal bezeichnet man die Eigenschaft, die dich bei einer statistischen Erhebung interessiert und die du erfasst. Nehmen wir an, du möchtest mit Hilfe einer Auszählung die beliebteste Autofarbe in deiner Straße herausfinden. Dafür bestimmst du für jedes Auto die Farbe und zählst für die verschiedenen Farben dann aus, wie viele Autos sie haben. Das ist statistisch nicht ganz genau – du weißt schließlich nicht, ob zum Beispiel alle Fahrer und Fahrerinnen von roten Autos gerade zu der Zeit weg sind, in der du zählst, – aber du kannst durch Zählungen zu verschiedenen Zeitpunkten deine Genauigkeit erhöhen. Die Farbe ist dann das Merkmal, das du erhebst. Du kannst natürlich noch weitere Merkmale oder auch Variablen erfassen, beispielsweise die Länge des Autos, das Baujahr oder die Zuordnung zu Klein-, Mittelklasse- und Oberklassefahrzeug. Diese verschiedenen Variablen unterscheiden sich im Skalenniveau, denn nicht mit allen kannst du die gleichen statistischen Operationen durchführen. Wir stellen dir die verschiedenen Skallenniveaus im Folgenden vor.
[quads id=1]Die verschiedenen Messniveaus im Vergleich
Nominalskala
Die Nominalskala ist das Skalenniveau mit den geringsten Anforderungen. Bei einer Nominalskala kannst du immer nur entscheiden, ob ein Merkmal eine bestimmte Ausprägung hat oder nicht. Du kannst die Ausprägungen aber nicht in einer feststehenden Reihenfolge anordnen oder mit ihnen rechnen. Die Ausprägungen unterscheiden sich nur von der Bezeichnung, vom Namen her – daher “Nominalskala”. Die Farbe der Autos ist ein klassisches Beispiel für eine Nominalskala. Du kannst sagen, ob ein Auto rot, blau oder grün ist. Du kannst diese Farben aber nicht der Größe nach sortieren oder in eine natürliche (mathematische) Reihenfolge bringen. blau ist nicht größer als grün. Du kannst mit diesen Farben auch nicht rechnen. So kannst du zum Beispiel keinen Mittelwert für die Farbe nennen, indem du alle in einen Topf wirfst und nachher als Mittelwert braun oder grau herauskommt. Für Merkmale, die du auf einer Nominalskala misst, kannst du nur die Anzahl der jeweiligen Ausprägungen bestimmen, und diese dann sortieren. Du kannst zum Beispiel sagen, dass blau die häufigste Autofarbe in deiner Straße ist. Das nennt man dann Modus oder Modalwert. Merkmale, die auf Ordinalniveau skaliert sind, lassen sich am besten in einem Balkendiagramm darstellen, also in einem Diagramm, bei dem die Merkmale von oben nach unten angeordnet sind und die Balken waagerecht liegen. Im Gegensatz zum Säulendiagramm geht man hier beim Anschauen nicht automatisch von einer Rangfolge der einzelnen Merkmale aus. Das Ganze könnte dann so aussehen:
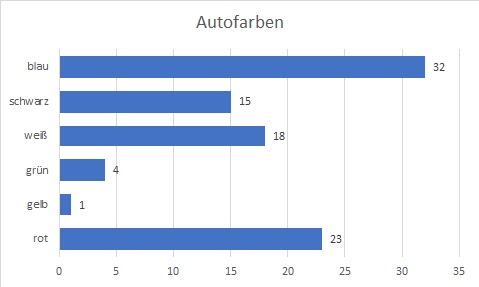
Weitere Beispiele für Merkmale, die nominales Messniveau haben, sind Geschlecht, Wohnort oder Telefonnummer.
Ordinalskala
Mit den Werten einer Ordinalskala kannst du zwar immer noch nicht rechnen, du kannst sie aber in eine Ordnung bringen. Wenn du die Autos in Größenklassen einteilst, kannst du diese sortieren und in eine Reihenfolge von klein nach groß bringen. Du kannst jedoch keine Durchschnittsgröße berechnen, solange du nur die Klassen verwendest. Dafür müsstest du die Längen richtig ausmessen, was du mit Hilfe einer Kardinalskala machen würdest. Die Werte einer Ordinalskala werden häufig durch Zahlen repräsentiert. Das kann verwirrend sein, weil du ja mit Zahlen rechnen kannst und deswegen vielleicht sofort vermutest, dass es sich um eine Kardinalskala handelt. Du kannst aber immer prüfen, ob es sich um eine Ordinalskala handelt, wenn du die Abstände zwischen den Zahlen untersuchst. Sind diese immer gleich groß? Oder sind sie gar nicht definiert und die Zahl steht eigentlich nur für die Position in der Rangfolge? Im zweiten Fall kannst du von einer Ordinalskala ausgehen. Diese kannst du in eine Ordnung bringen – mehr aber auch nicht. Beispielsweise sind Schulklassen ordinal skaliert. Das bedeutet, dass du sie sortieren kannst. Aber die vierte Klasse ist nicht das Doppelte der zweiten Klasse. Dasselbe gilt übrigens für Schulnoten. Eine 2 ist nicht doppelt so gut wie eine 4, und der Abstand zwischen einer 1 und einer 2 ist nicht derselbe wie der zwischen einer 5 und einer 6. Die Zahlen repräsentieren hier nur die Reihenfolge der Noten sehr gut, gut usw. Aus diesem Grund ist es aus statistischer Sicht übrigens falsch (und unsinnig) Durchschnittsnoten zu errechnen. Man rechnet hier nämlich mit Rängen und nicht mit wirklichen Zahlen. Es wird aber trotzdem immer wieder gemacht. Wenn du einen mittleren Wert für eine Ordinalskala berechnen willst, kannst du den Median ausrechnen. Dafür sortierst du alle Messergebnisse in der Rangfolge des erhobenen Merkmals und suchst den Wert, der genau in der Mitte liegt. 50% aller Messergebnisse sollen unter dem Median liegen und 50% darüber. In der folgenden Schulnotenübersicht liegt der Median bei 3.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 8 | 5 | 3 | 1 |
Als Diagramm für ein ordinales Messniveau eignet sich ein Säulendiagramm.
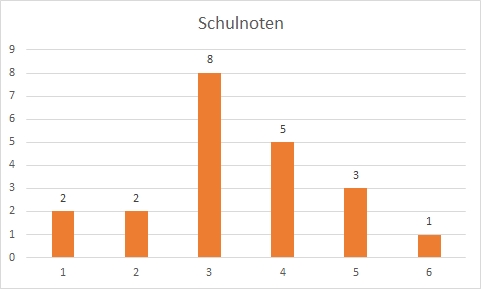
Weitere Beispiele für Ordinalskalen sind alle Formen von Rangfolgen sowie die Erhebung in Marktstudien mit Skalen von zum Beispiel 1 bis 5. Auch bei diesen werden regelmäßig fälschlicherweise arithmetische Mittel und sogar Streuungsmaße ausgerechnet.
Kardinalskalen
Mit Kardinalskalen oder metrischen Skalen kannst du nun rechnen und etliche statistische Operationen durchführen. Man unterscheidet hier noch einmal zwei Unterskalen, die aber kaum Einfluss auf die statistische Einordnung haben.
Intervallskala
Bei einer Intervallskala sind die Abstände (Intervalle) zwischen den einzelnen Punkten der Skala gleich groß. Außerdem kann man auch zwischen den ganzen Werten messen. Dies ist immer der Fall, wenn deine Skala eine Einheit hat. Wenn du die Länge in Meter misst, ist der Abstand zwischen einem Meter und zwei Metern genauso groß wie zwischen vier und fünf Metern. Außerdem kannst du auch eine Länge von 3,45 Metern angeben und jeder weiß genau, was du damit meinst. Aus diesem Grund kannst du mit den Werten einer Intervallskala rechnen. Du kannst beispielsweise das arithmetische Mittel bilden. Dazu summierst du alle einzelnen Messwerte und teilst das Ergebnis durch die Anzahl der Messwerte. Damit weißt du, wie lang beispielsweise das (nur gedachte) durchschnittliche Auto deiner Messung ist. Als grafische Darstellung wird häufig das Histogramm gewählt. Es sieht auf den ersten Blick wie ein Säulendiagramm aus. Der Unterschied ist jedoch, dass die Messergebnisse in Klassen eingeteilt werden und die Anzahl der Werte in der jeweiligen Klasse als Fläche angezeigt wird. Dies kann zum Beispiel wie unten aussehen. Die Breite der verschiedenen Klassen ist hier gleich gewählt und mit jeweiliger Ober- und Untergrenze angegeben.
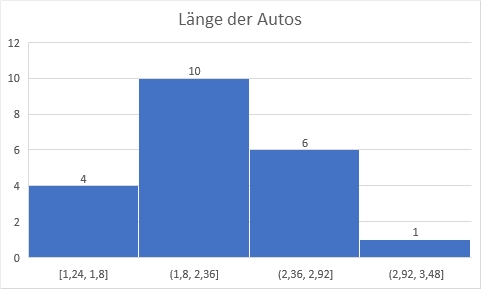
Verhältnisskala
Die Verhältnisskala unterscheidet sich von der Intervallskala nur dadurch, dass sie einen natürlichen Nullpunkt besitzt. Dies ist zum Beispiel bei der Länge der Fall oder bei der Berechnung einer Dauer, nicht jedoch beim Datum.
