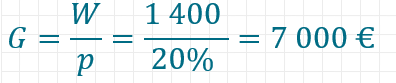In diesem Artikel erfährst du alles, was du über Prozentrechnung wissen musst.
Was ist Prozentrechnung?
Der Begriff „Prozent“ kommt aus dem Lateinischen und bedeutet ganz einfach „für Hundert“ bzw. „pro Hundert“. Du kannst also mit Hilfe der Prozentrechnung angeben, welchen Anteil eine bestimmte Menge rein rechnerisch an 100 hätte. Man macht das, um Dinge miteinander vergleichbar zu machen. Wenn du eine Zahl mit „Prozent“ kennzeichnest, heißt das mathematisch, dass du sie durch 100 teilst. 20% ist also derselbe Wert wie 0,2.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=1]
[su_divider top=“no“ divider_color=“#eeeeee“]
Wenn du beispielsweise wissen möchtest, welcher Anteil am Einkommen in einem bestimmten Land für Lebensmittel ausgegeben wird, hast du viele verschiedene Einflussfaktoren, die dieses Verhältnis in den beiden Ländern bestimmen: die Lebensmittelpreise, die Höhe eines normalen Gehalts, die Menge und Art an Lebensmitteln, die in diesem Land konsumiert werden und so weiter. Wenn du es also ganz einfach und vergleichbar machen willst, hebelst du all diese Einflussfaktoren aus, indem du einfach angibst, wie viel „pro Hundert“ jeweils ausgegeben wird, also wie viel Euro von 100 Euro Gehalt in Lebensmittel gesteckt werden. Dies kannst du dann mit dem Prozentzeichen (%) kennzeichnen, also zum Beispiel 23 %.
Welche Begriffe brauchst du für die Prozentrechnung?
In der Prozentrechnung brauchst du genau drei Werte, den Prozentsatz, den Grundwert und den Prozentwert.
Nehmen wir an, in unserem obigen Beispiel beträgt das durchschnittliche Einkommen in Land A 3 500 Euro. Pro Monat geben die Menschen durchschnittlich 1 312,50 Euro für Lebensmittel aus. Nun willst du wissen, wie viel Prozent das sind. Die 3 500 Euro sind der Grundwert (G), er entspricht immer 100 %. Der Prozentwert (W) ist 1 312,50 Euro, es ist der Anteil am Grundwert, den du mit dem Prozentsatz (p) bestimmen möchtest.
Wie du die einzelnen Werte mithilfe der Prozentrechnung ausrechnen kannst
Prozentrechnung ist eine besondere Anwendung für den Dreisatz, du kannst also eine Aufstellung wie folgt machen:
Grundwert → 100 %
Prozentwert → Prozentsatz
Mit dieser Aufstellung und den Regeln für den Dreisatz (oder unserem Dreisatz-Rechner) kannst du alle Aufgaben in der Prozentrechnung lösen. In jeder Aufgabe hast du zwei der drei der Werte Grundwert, Prozentwert und Prozentsatz gegeben. Wenn du diese in das Schema oben richtig einordnest, kannst du die Aufgabe ganz einfach lösen. Im Folgenden findest du für jede Variante ein Beispiel.
Grundwert und Prozentwert gegeben, Prozentsatz gesucht
Die Aufgabe, die wir oben bereits begonnen haben, hat den Grundwert (3 500 Euro) und den Prozentwert (1 312,50 Euro). Gesucht ist der Prozentsatz. Dein Schema sieht also wie folgt aus:
3 500 Euro → 100%
1 312,50 → ?
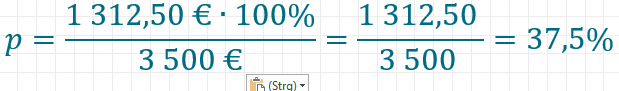
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=2]
[su_divider top=“no“ divider_color=“#eeeeee“]
Da 100 % genau 1 entspricht und du bei Multiplikation mit 1 und Division durch 1 immer beim selben Ergebnis bleibst, kannst du diesen Teil in den Berechnungen auch einfach weglassen. Es gilt also:
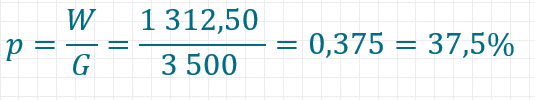
Grundwert und Prozentsatz gegeben, Prozentwert gesucht
Wenn du nun weißt, dass in Land B 30 % des Einkommens für Lebensmittel ausgegeben werden, und das mittlerre Einkommen 4 000 Euro beträgt, kannst du ausrechnen, welcher Prozentwert W absolut gesehen für Lebensmittel verwendet wird. Deine Aufstellung lautet dann:
4 000 Euro → 100%
? → 30%
Die Berechnung ist genau so einfach wie eben und du wendest nur den Dreisatz an. Auch hier kannst du die 100 % einfach weglassen, weil sie das Ergebnis nicht verändern.
W = G • p = 4 000 • 30% = 1 200
Prozentwert und Prozentsatz gegeben, Grundwert gesucht
Von einem dritten Land C erfährst du nun, dass dort nur 20% des mittleren Einkommens für Lebensmittel ausgegeben werden, dass dies in Summe aber 1 400 Euro sind. Wie hoch ist das mittlere Einkommen in diesem Land? Du suchst hier nun den Grundwert G.
? → 100%
1 400 Euro → 20%
Die Berechnung mittels Dreisatz kannst du dann wie folgt lösen: