Im Mathe-Unterricht musst du nicht nur rechnen, manchmal musst du auch geometrische Figuren zeichnen. Dabei ist es sehr wichtig, dass du besonders genau vorgehst, damit wirklich alle Maße übereinstimmen und du das, was du ausrechnest, später auch nachmessen kannst. Daher haben wir für dich ein paar Tipps zusammengestellt, wie du einfacher und genauer geometrische Figuren zeichnen kannst.
Was brauchst du, um geometrische Figuren zu zeichnen?
Um Kreise, Dreiecke und Co. zu zeichnen, brauchst du gar nicht viel. Ein paar Dinge sind aber wirklich wichtig. Wenn du alles hast, was auf der folgenden Liste steht, kannst du loslegen.
- kariertes Papier (zum Beispiel dein Heft),
- Bleistift,
- Radiergummi,
- Bleistift-Spitzer,
- Lineal,
- Geodreieck,
- Zirkel.
Am besten gewöhnst du dir gleich an, immer nur mit dem Bleistift zu zeichnen, und am besten nur, wenn er gut gespitzt ist. Denn alles, was du mit Füller oder Kugelschreiber zeichnest, wird ungenauer, und du kannst es außerdem nicht mehr so gut korrigieren.
[quads id=1]Natürlich kannst du auf jedem Papier zeichnen. Kariertes Papier hiflt dir aber zum einen, sowohl senkrecht als auch waagerecht gerade zu zeichnen. Zum anderen hast du bezüglich Längen und Breiten direkt eine Orientierungshilfe, weil ein Kästchen normalerweise 0,5 cm breit ist.
Ein Koordinatensystem zeichnen
Wenn du Punkte, Strecken oder Geraden zeichnen sollst, werden dir oft Punkte für ihre Lage angegeben, die du in einem Koordinatensystem eintragen sollst. Ein Koordinatensystem besteht aus zwei im rechten Winkel zueinander stehenden Linien, die über ihre ganze Länge “durchnummeriert” sind. Im Grunde sind die beiden Achsen des Koordinatensystems zwei Zahlenstrahlen, wie du sie bereits seit der Grundschule kennst. Die x-Achse ist immer die waagerechte Achse, die y-Achse die senkrechte. Du kannst dir das einfach so merken, dass du mit der Achse beginnst, die du auch zuerst als Zahlenstrahl kennengelernt hast, und diese hat auch den früheren Buchstaben im Alphabet.
Um ein Koordinatensystem zu zeichnen, beginnst du zunächst mit der x-Achse, die du möglichst mittig auf dein Blatt setzt. Du brauchst dafür nicht mehr als dein Lineal und deinen Bleistift, denn du kannst dich sehr gut an den Kästchen auf deinem karierten Papier orientieren. Suche dir eine Linie aus, die ungefähr in der Mitte des Blatts liegt, lege dein Lineal an diese Linie und ziehe dann deine x-Achse dorthin. Ans rechte Ende des Achse kommt eine Pfeilspitze. Nun zeichnest du ungefähr in die Mitte der x-Achse eine senkrechte Linie, die die x-Achse schneidet. Dies ist deine y-Achse. Auch hier kannst du dich wieder an den Linien in deinem Heft orientieren. Auch die y-Achse erhält eine Pfeilspitze, und zwar ans obere Ende.
[quads id=2]Nun zeichnest du noch im Abstand von 1 cm (also 2 Kästchen) auf beiden Geraden die einzelnen Punkte ein und nummerierst sie durch. Der Schnittpunkt der beiden Achsen ist die 0, rechts bzw. oberhalb des Nullpunkts beginnst du mit 1 und zählst weiter, links oder unterhalb der Null fängst du mit -1 an und setzt die Reihe dann entsprechend fort. Dieses Koordinatensystem kannst du nun nutzen, um Punkte und Strecken hinein zu zeichnen.
Einen Punkt im Koordinatensystem eintragen
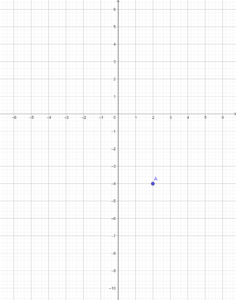
Punkte zeichnest du eigentlich immer in ein Koordinatensystem ein, denn ansonsten kannst du ja einfach einen Punkt auf ein Blatt Papier setzen und bist bereits fertig. Die Lage von Punkten wird dann zum Beispiel so angegeben: A(2,-4). Der Punkt A liegt dann auf der x-Achse bei 2 und auf der y-Achse bei -4. Um ihn einzuzeichnen, beginnst du beim Nullpunkt und bewegst dich auf der x-Achse zum ersten angegebenen Punkt. Da dieser im Beispiel positiv ist, bewegst du dich nach rechts zur 2. Von dort zählst du dann so viele Schritte nach oben oder unten, bis du beim Punkt auf der y-Achse angekommen bist. Da der Punkt im Beispiel negativ ist, zählst du 4 Schritte nach unten. Dort setzt du dann deinen Punkt hin. Wenn du nur einen Punkt zeichnen sollst, kannst du diesen auch mit einem bunten Stift (Holzbuntstift oder Fineliner) einzeichnen, weil man ihn sonst im Koordinatensystem nicht gut erkennen kann.
Strecken, Halbgeraden und Geraden zeichnen
Strecken, Halbgeraden (bzw. Strahlen) und Geraden zeichnest du normalerweise ebenfalls im Koordinatensystem. Der Unterschied zwischen den dreien ist sehr einfach: Strecken haben einen Anfang und ein Ende, Halbgeraden nur eines davon und Geraden weder einen Anfang noch ein Ende. Da du nicht unendlich lange geometrische Figuren zeichnen kannst, kannst du den endlosen Verlauf einer Gerade oder Halbgerade nur andeuten. Im Koordinatensystem macht man dies normalerweise auch mit Hilfe von Punkten. Denn der Verlauf von Geraden, Halbgeraden und Strecken wird immer durch zwei Punkte angegeben. Für Strecken sind dies meist Anfangs- und Endpunkt. Für Geraden sind dies einfach zwei Punkte durch die die Gerade läuft, sodass du sie vor und hinter den Punkten noch verlängern kannst.
Normalerweise erhältst du also als Information die Lage von zwei Punkten. Wir nehmen hierzu A(2,-4) von eben und außerdem B(-1,1). Diese zeichnest du beide in dein Koordinatensystem ein. Dann legst du dein Lineal genau durch beide Punkte. Wenn du eine Strecke zeichnen sollst, verbindest du die Punkte einfach miteinander. Bei einer Halbgeraden setzt du sie durch einen Punkt weiter fort. Für eine Gerade führst du die Linie hinter beiden Punkten fort. Das Beispiel unten zeigt eine Halbgerade, damit du für beide Varianten erkennen kannst, wie es im Koordinatensystem aussieht.
Kreise zeichnen
Kreise kannst du nur mit dem Zirkel zeichnen, daher solltest du diesen immer dabei haben, wenn ihr in der Schule gerade geometrische Figuren zeichnen sollt.
Ein Kreis wird durch zwei Informationen exakt bestimmt, und genau diese Informationen benötigst du auch, um ihn zu zeichnen: Die Lage des Mittelpunkts und den Radius. Sollte in einer Aufgabe der Durchmesser und nicht der Radius angegeben sein, berechnest du am besten erst einmal den Radius, indem du den Durchmesser durch 2 teilst. Danach wird das Zeichnen deutlich einfacher. Markiere zunächst den Mittelpunkt (wir nehmen A(2,-4) aus unserem Beispiel) im Koordinatensystem oder auf einem Blatt. Dann misst du mit dem Zirkel und deinem Lineal die Strecke des Radius ab. Wenn du einen Kreis mit r = 3 cm zeichnen sollst, legst du dein Lineal auf ein Blatt Papier und steckst die Spitze bei der 0 ein. Dann stellst du den Zirkel so ein, dass der Bleistift des Zirkels bei 3 cm liegt.
Als nächstest steckst du die Spitze des Zirkels in den Mittelpunkt, den du bereits gezeichnet hast. Nun kannst du den Bleistift des Zirkels einfach aufs Blatt setzen und mit möglichst leichtem Druck (um den Zirkel nicht aus Versehen zu verstellen), deinen Kreis einzeichnen.
Dreiecke und Vierecke zeichnen
Wenn du Dreiecke oder Vierecke im Koordinatensystem zeichnen sollst, trägst du zunächst alle angegebenen Punkte ein und verbindest diese dann in der Reihenfolge, wie die Punkte im Alphabet vorkommen.
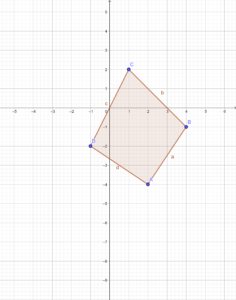
Manchmal zeichnest du solche Figuren jedoch nicht im Koordinatensystem, sondern erhältst andere Angaben, zum Beispiel “Zeichne ein rechtwinkliges Dreieck” oder “Zeichne ein Quadrat mit einer Seitenlänge von 2 cm”. In diesem Fall musst du auf dein Geodreieck zurückgreifen und nicht nur die Seitenlängen abmessen, sondern auch die zugehörigen WInkel. Bei einem rechten Winkel ist dies besonder einfach, weil du das Geodreieick einfach mit der Spitze in den entsprechenden Punkt legen musst und zu beiden Seiten eine Linie zeichnen kannst. Andere Winkel musst du genauer abmessen, diese sind jedoch im Geodreieck eingezeichnet.
Wie hilfreich war dieser Beitrag?
Klicke auf die Sterne um zu bewerten!