Winkelfunktionen, die auch trigonometrische Funktionen genannt werden, sind Zusammenhänge zwischen Winkeln und den Verhältnissen der Längen von Seiten. Anwendung finden diese Funktionen im Bereich der Vermessung, des Maschinenbaus und in der Physik. Ursprünglich definiert wurden diese Funktionen über die Seiten von Dreiecken, später folgte eine Definition über den Kreis.
Hinweis
In diesem Artikel wird häufig der Winkel Alpha als spitzer Winkel in einem Dreieck mit rechtem Winkel verwendet, dabei muss es sich aber nicht um den kleineren der beiden Winkel ungleich 90° handeln.
Winkelfunktionen im rechtwinkligen Dreieck
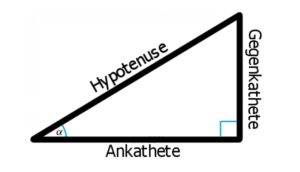
Eine sehr wichtige Definition der Winkelfunktionen bezieht sich auf die Verhältnisse der Längen verschiedener Seiten eines rechtwinkligen Dreiecks zu dessen Winkeln.
Vom Winkel Alpha aus gesehen liegt die Gegenkathete gegenüber dem Winkel, die Ankathete schließt an den Winkel an und die Hypotenuse ist im rechtwinkligen Dreieck immer gegenüber dem 90° Winkel.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=1]
[su_divider top=“no“ divider_color=“#eeeeee“]
Wenn wir das Verhältnis der Länge der Gegenkathete von Alpha zur Hypotenuse betrachten, erhalten wir den Sinus von Alpha.
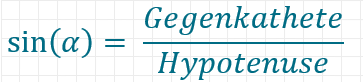
Für jeden Winkel Alpha ist dieses Verhältnis gleich, denn zwei rechte Dreiecke mit einem gleichen Winkel haben automatisch (Winkelsumme 180° – 90° – Winkel = anderer Winkel) auch den dritten Winkel gemeinsam und sind sich ähnlich.
Das gilt natürlich auch für die anderen beiden grundlegenden Winkelfunktionen. Hier siehst du alle drei im Überblick:

Hinweis:
Der Vulkan SohCahToa hilft dir bei Trigonometrie. Wenn S der Sinus, C der Cosinus und T der Tangens ist, dann ergeben sich die Funktionen für einen Winkel aus den Buchstaben danach.
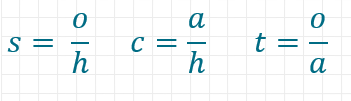
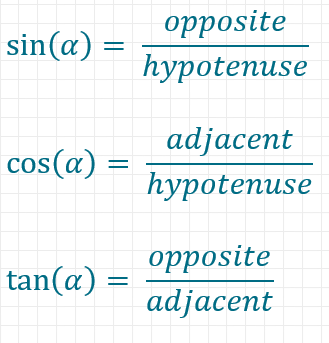
Dabei gilt für die englischen Wörter:
Adjacent = Ankathete
Hypotenuse = Hypotenuse
Opposite = Gegenkathete
Bei den Anfangsbuchstaben gibt es nur bei Opposite und Gegenkathete einen anderen, so kann man sich die englische Eselsbrücke gut merken.
Beispiele
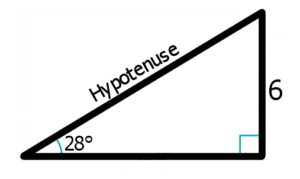
Betrachten wir das Dreieck
Wie lang ist die Hypotenuse?
Welche Seiten hast du gegeben? Gegeben ist die Seite gegenüber dem Winkel, du hast also eine Gegenkathete mit einer Länge von 6. Wenn du einen Winkel und dessen Gegenkathete kennst und die Hypotenuse suchst, wo kannst du dann einen Zusammenhang dieser drei Zahlen finden?
Beim Sinus:
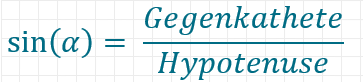
Du kannst also einsetzen:
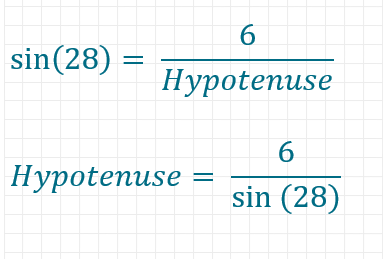
Da sich Winkelfunktionen nur sehr mühsam von Hand berechnen lassen, kannst du den Taschenrechner verwenden. Die Hypotenuse ist etwa 12,8 Einheiten lang.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=2]
[su_divider top=“no“ divider_color=“#eeeeee“]
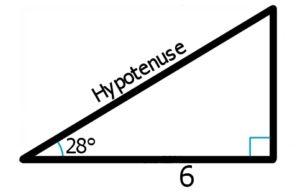
Wie lang ist die Hypotenuse?
Wieder kannst du dir einfach aus den Winkelfunktionen die passende heraussuchen. Diesmal hast du Werte für den Cosinus.
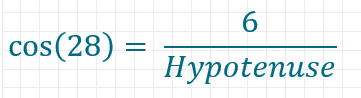
Nach etwas umformen erhältst du für die Hypotenuse etwa 6,79 Längeneinheiten.
Vorsicht: Bei Winkelfunktionen geht es um Ähnlichkeit. Dieses Dreieck ist zwar ähnlich zu dem aus dem vorigen Beispiel, es ist aber deutlich kleiner.
Du kannst Aufgaben dieser Art immer bequem lösen. Sieh dir einfach an, was gegeben ist und finde eine Winkelfunktion, die den Zusammenhang aus gegebenen und gesuchten Zahlen beschreibt.
Umkehrfunktionen
Was aber, wenn du ein Seitenverhältnis hast und den dazu passenden Winkel suchst?
Hat ein rechtwinkliges Dreieck z.B. zum Winkel Alpha die Hypotenuse mit 6 Längeneinheiten und die Gegenkathetenlänge 2,5, dann hat es den Winkel:
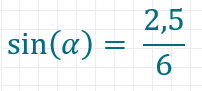
Der Zusammenhang ist zwar richtig, doch du suchst nicht den Sinus des Winkels, sondern den Winkel, dessen Sinus dem Verhältnis entspricht. Was du benötigst ist eine Umkehrfunktion.
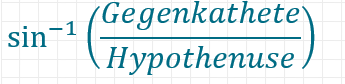
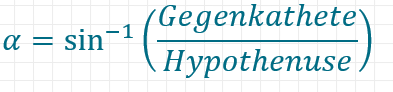
Im Beispiel also
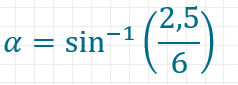
Im Taschenrechner kannst du das meist mit einer Umkehrtaste Inv und dem Sinus machen. Es ergibt sich ein Winkel von etwa 24,62°
Zusammenfassung:
Winkelfunktionen haben Winkel als Eingabewert und ergeben Seitenverhältnisse.

Umkehrfunktionen der Winkelfunktionen haben Seitenverhältnisse als Eingabewert und ergeben Winkel, man nennt solche Funktionen auch Arkusfunktionen.

Vorsicht!
Die Umkehrfunktion einer Winkelfunktion ist nicht deren Kehrwert.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=3]
[su_divider top=“no“ divider_color=“#eeeeee“]
Komplementäre Funktionen
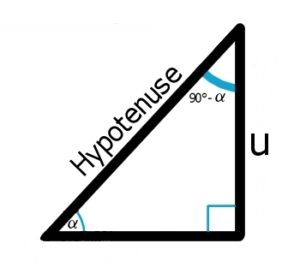
Zu den Winkelfunktionen gibt es Kofunktionen. Hier als Beispiel Sinus und Cosinus.
Wegen der Winkelsumme von 180° ergibt sich im rechten Dreieck für einen bekannten Winkel Alpha ein zweiter spitzer Winkel von 90°-Alpha.
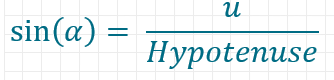
Für den Cosinus des Winkels 90°-Alpha ergibt sich
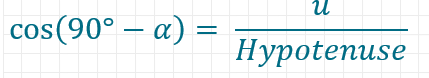
Das Seitenverhältnis des Sinus von Alpha ist genau gleich zum Cosinus des anderen spitzen Winkels.
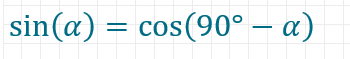
Auch andere Winkelfunktionen haben Kofunktionen. Den Sekans lernst du später kennen, für die Vollständigkeit ist er aber hier schon mal dabei.
Beispiel
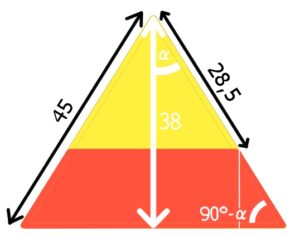
Anna taucht einen Tortilla, der symmetrisch zur vertikalen Achse ist, ganz genau dieser Achse entlang in einen scharfen Dip.
Wie tief (Gesamthöhe des Tortilla = 38mm) hat Anna den Tortilla eingetaucht?
Da der Tortilla symmetrisch ist, kannst du annehmen, dass die Seite, von deren Länge 28,5mm außerhalb des Dips sind, insgesamt eine Länge von 45mm hat. Für den Winkel Alpha hast du also die Ankathete und die Hypotenuse, das ist der Kosinus.
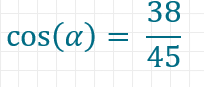
Wenn der Tortilla h cm tief in den Dip getaucht ist, dann ist die Höhe außerhalb des Dips 38-h cm. Im kleinen gelben Dreieck rechts der Mitte gilt:
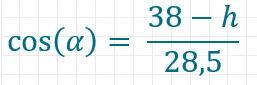
Da beide Verhältnisse gleich sein müssen, da es je um den gleichen Winkel Alpha geht, kannst du sie gleichsetzen.
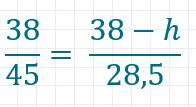
Für h ergeben sich etwa 13,9mm.
Alternativ könntest du auch den Zusammenhang
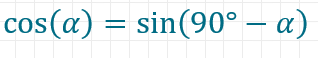 verwenden. Das kleine Dreieck rechts unten mit der Hypotenuse 45-28,5 und dem Winkel 90°-Alpha hat die gesuchte Höhe als Gegenseite zum Winkel 90°-Alpha.
verwenden. Das kleine Dreieck rechts unten mit der Hypotenuse 45-28,5 und dem Winkel 90°-Alpha hat die gesuchte Höhe als Gegenseite zum Winkel 90°-Alpha.
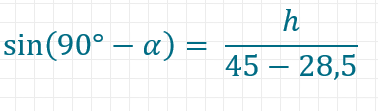
Durch Gleichsetzen erhältst du
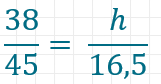
Für h erhältst du natürlich das gleiche Ergebnis wie vorher.
Sinussatz
Im Gegensatz zu den bisherigen Gesetzen, die für rechtwinklige Dreiecke gelten, kannst du den Sinussatz für beliebige Dreiecke anwenden. Der Satz beschreibt die Tatsache, dass das Verhältnis zwischen dem Sinus eines Winkels und der Dreiecksseite gegenüber diesem Winkel für alle Paare aus Winkeln und deren Gegenseiten in einem Dreieck gleich ist.
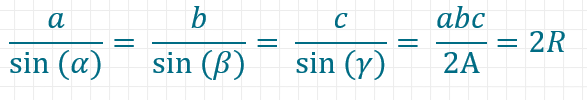
Dabei sind A der Flächeninhalt und R der Umkreisradius des Dreiecks.
Beispiel
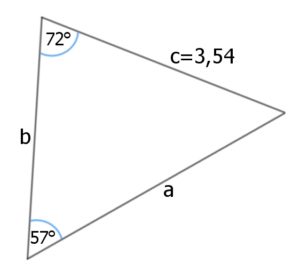
Bei einer Landvermessung wird ein dreieckiges Feld zwischen zwei Straßen vermessen. Um nicht die ganze Strecke ablaufen zu müssen, wird nur eine Seite wirklich gemessen. Ermittle die Längen von a und b.
Gegeben ist das Verhältnis von Seite c (3,54 Kilometer) zu 57°.
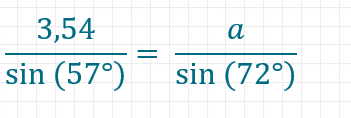
Für a ergibt sich etwa 4,01km als Länge. Genau so kannst du auch die fehlende Seite b berechnen.
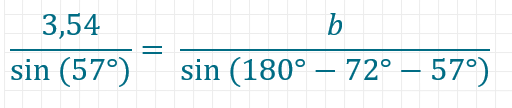
Für b erhältst du etwa eine Länge von 3,28km.
Auch wenn dir der Taschenrechner sehr viele Stellen nach dem Komma zeigt, sind die Messwerte vermutlich nicht genau genug für solche Antworten, runde also deine Antworten auf eine sinnvolle Genauigkeit.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=1]
[su_divider top=“no“ divider_color=“#eeeeee“]
Kosinussatz
Der Kosinussatz beschreibt einen Zusammenhang zwischen den drei Seiten eines Dreiecks und dem Kosinus eines Winkels und zwei Dreiecksseiten.
c2 = a2 + b2 -2 • a • b • cos(γ)
Für die anderen Seiten tauscht das c den Platz mit der jeweils gesuchten Seite in der Gleichung.
b2 = a2 + c2 -2 • a • c • cos(β)
a2 = b2 + c2 -2 • b • c • cos(α)
Das sieht alles verdächtig nach dem Satz des Pythagoras aus und da bei einem rechtwinkligen Dreieck der Kosinus des rechten Winkels 0 ergibt, lautet der Kosinussatz für die Hypotenuse:
c2 = a2 + b2