Ob es um radioaktiven Zerfall, das Wachstum einer Bakterienpopulation oder Zinsen auf einem Konto geht, Exponentialfunktionen und Logarithmen begegnen dir in Natur und Gesellschaft häufig. Dieser Artikel erklärt dir die wichtigsten Eigenschaften der Logarithmusfunktionen. Ein Verständnis von Exponentialfunktionen ist für diesen Artikel notwendig.
Was ist der Logarithmus?
Der Logarithmus einer Zahl ist der positive Exponent, mit dem eine positive Basis potenziert werden muss, um die gegebene Zahl zu erhalten.
Der Logarithmus der Zahl a wäre die Zahl x, welche die Gleichung bx = a löst.
Geschrieben wird diese Umkehrung des Potenzierens für eine eindeutige Lösung als x = logba
Man bezeichnet das als den Logarithmus von a zur Basis b.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=1]
[su_divider top=“no“ divider_color=“#eeeeee“]
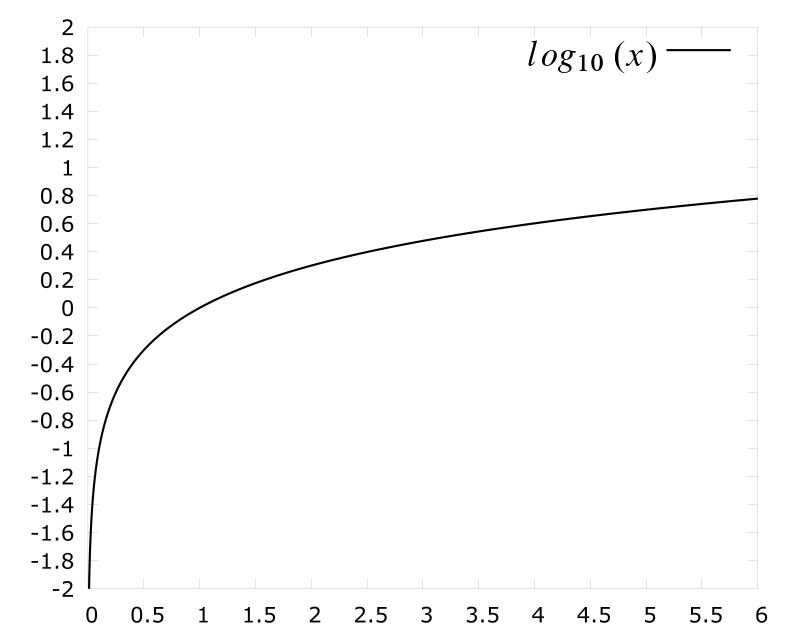
Die Funktionsgleichung einer Logarithmusfunktion ist y = loga x mit positiven reellen Zahlen ungleich 1 als a und positiven reellen Zahlen als x.
Definition
Der Logarithmus ist die Umkehrfunktion der Exponentialfunktion.
Für eine positive Basis b gilt:
bx und logbx sind Umkehrfunktionen.
Die Funktionen machen einander rückgängig.
Wenn du eine der Funktionen für x in eine andere einsetzt, erhältst du x als Ergebnis.
bx kommt für x in logbx und logbx wandert als x zu bx.
b(logbx) = x und logbbx = x
103 = 1000 und log101000 =3
Beispiel
Berechne den Logarithmus von 64 zur Basis 8.
x = log8 64, das entspricht der Frage, mit welcher Zahl du 8 potenzieren musst, um 64 zu erhalten.
x = log8 64 = 2, denn 82 = 64
Vorsicht
Auf dem Taschenrechner steht die Taste log meist für den dekadischen Logarithmus mit der Basis 10.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=2]
[su_divider top=“no“ divider_color=“#eeeeee“]
Der dekadische Logarithmus
Der dekadische Logarithmus hat eine Basis von 10. Obwohl eigentlich nicht eindeutig, wird er in der Praxis häufig einfach nur als log geschrieben, korrekt wäre lg.
Mit der Basisumrechnung kannst du Logarithmen zu einer anderen Basis (a) ausrechnen
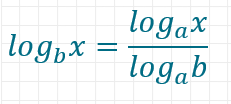
Beispiel
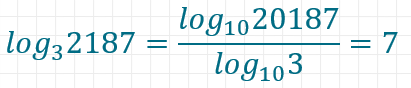
So könntest du mit deinem Taschenrechner mit dem dekadischen Logarithmus einen Logarithmus zur Basis 3 ausrechnen.
Der natürliche Logarithmus
Der Logarithmus mit der Basis e (siehe oben) wird als natürlicher Logarithmus bezeichnet und meist mit ln abgekürzt.
Wenn y=ex dann x=ln y
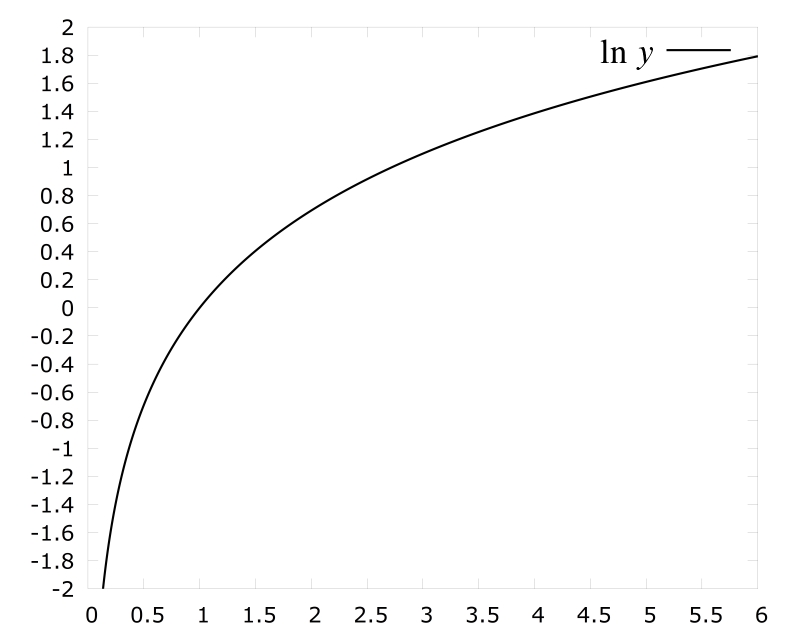 Bei y=1 (hier ist y auf der horizontalen Achse), hat der natürliche Logarithmus den Wert 0, bei e den Wert 1.
Bei y=1 (hier ist y auf der horizontalen Achse), hat der natürliche Logarithmus den Wert 0, bei e den Wert 1.
Definition des natürlichen Logarithmus
Der natürliche Logarithmus ln einer Zahl a kann als Fläche unter der Hyperbel 1/x definiert werden.
Es gilt für a = e : ln(a) = 1 $
Für Werte von a < 1 wird die Fläche negativ gezählt, es ergibt sich ein negativer natürlicher Logartithmus, siehe auch den Plot des natürlichen Logarithmus.
Rechenregeln
Produkte von Logarithmen lassen sich sehr einfach zerlegen.
Der Logarithmus eines Produkts ergibt sich aus der Addition der Logarithmen der Faktoren
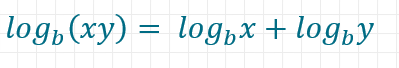
Der Logarithmus eines Quotienten ergibt sich wie folgt:
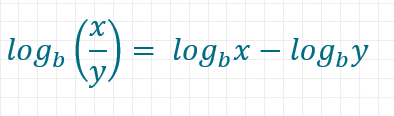
Logarithmen von Potenzen mit reellen Exponenten folgen der Regel
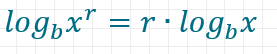
Daraus folgt für negative Exponenten, dass
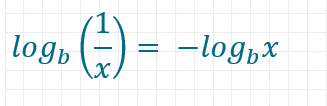
Wurzeln lassen sich wie folgt umwandeln:
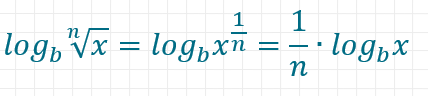
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=3]
[su_divider top=“no“ divider_color=“#eeeeee“]
Analytische Eigenschaften
- Für eine Basis a kleiner als 1 ist der Graph von f(x)= \logax streng monoton fallend, für eine Basis a größer als 1 streng monoton steigend. Bei beiden Varianten nähert sich der Graph der y-Achse an, hat diese also als senkrechte Asymptote der Logarithmuskurve.
- Logarithmusfunktionen haben keinen y-Achsenabschnitt und schneiden (siehe oben) die x-Achse im Punkt (1|0).
Sollte die Funktion natürlich durch eine Konstante verschoben sein, so ändert sich auch der Schnittpunkt mit der x-Achse. - Integration: Das unbestimmte Integral des natürlichen Logarithmus ist
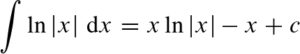
Fazit
In diesem Artikel hast du einen Überblick über besonders wichtige Eigenschaften von Logarithmusfunktionen erhalten. Es gibt über diese Funktionen noch viel mehr zu wissen, doch solltest du mit dem hier dargestellten Wissen viele Aufgaben lösen können.