Wie du Gleichungen löst, weißt du wahrscheinlich schon. Lineare Gleichungssysteme bestehen aus mehreren linearen Gleichungen mit mehreren Variablen. Du kannst sie nur gemeinsam lösen.
Was ist ein lineares Gleichungssystem?
Ein lineares Gleichungssystem (häufig als LGS abgekürzt) besteht aus zwei oder mehr linearen Gleichungen mit mehr als einer Variable. Das bedeutet, dass alle Variablen nur mit dem Exponenten 1 vorkommen.
Meist wirst du mit LGS mit zwei Gleichungen und zwei Variablen zu tun haben. Diese sehen dann zum Beispiel wie folgt aus:
2x + 2y = 4
5x – y = 10
Statt x und y werden häufig auch x1 und $x2 als Variablennamen verwendet. Die Lösung funktioniert genau gleich. Ein lineares Gleichungssystem aus zwei Gleichungen mit zwei Variablen lässt sich sehr gut geometrisch darstellen, wie wir im nächsten Abschnitt zeigen.
[quads id=1]Lineare Gleichungssysteme im Koordinatensystem
Lineare Gleichungen mit den beiden Variablen x und y hast du sicher schon vorher im Mathe-Unterricht kennengelernt, nämlich als lineare Funktionen, die du als Gerade im Koordinatensystem darstellen kannst. Diese haben die Form y = ax + b. Da du weißt, dass sich Gleichungen leicht umformen lassen, bilden lineare Gleichungen mit zwei Variablen die Grundlage für lineare Funktionen. Du kannst sie also graphisch im Koordinatensystem darstellen.
Dazu formst du die Gleichungen zunächst um. Für das obige Beispiel kannst du genauso gut schreiben:
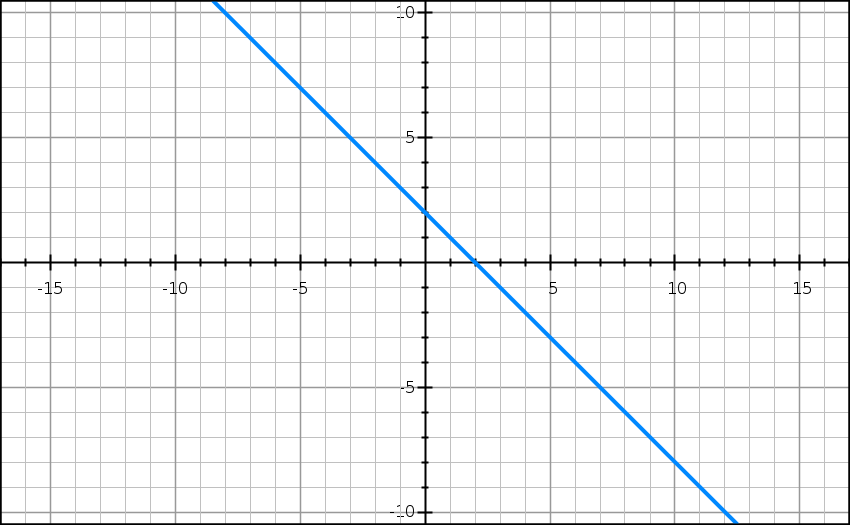
y = -x + 2
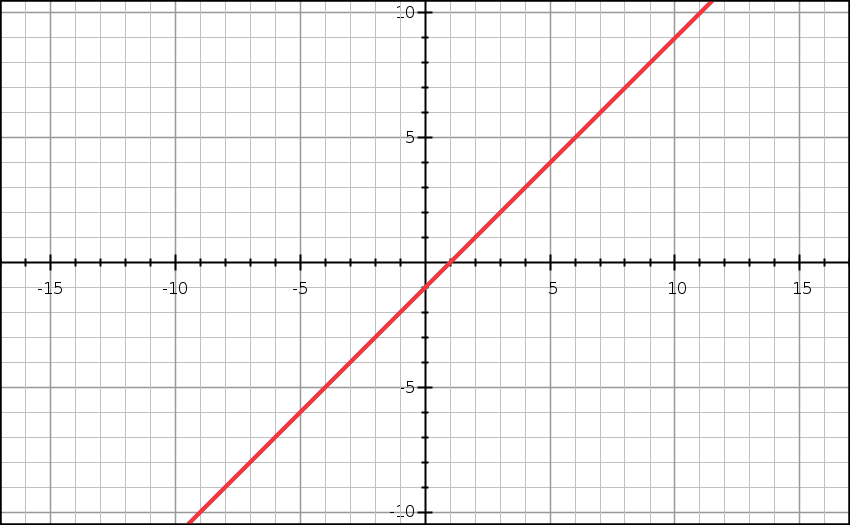
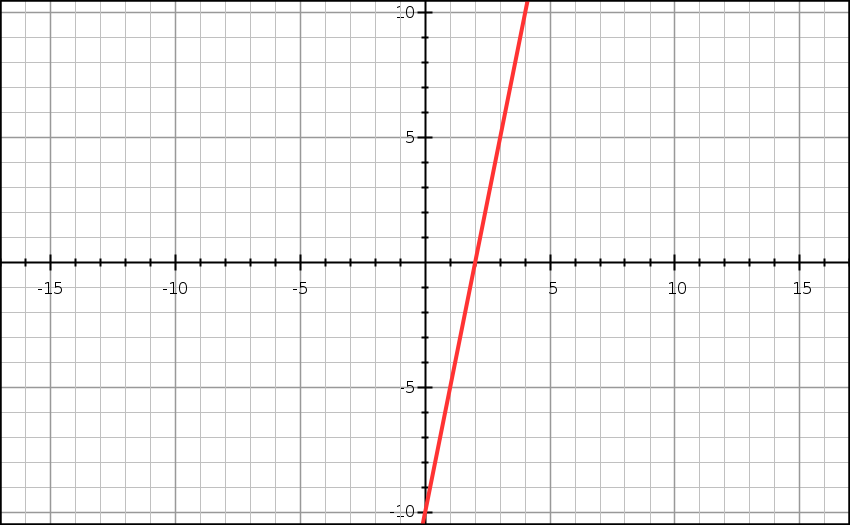
y = 5x – 10
Diese Geraden kannst du im Koordinatensystem abtragen.
y = -x + 2:
y = 5x – 10:
Wenn du ein lineares Gleichungssystem löst, suchst du Werte für x und y, für die beide Gleichungen gültig sind. Geometrisch ausgedrückt ist dies der Schnittpunkt der beiden Geraden:
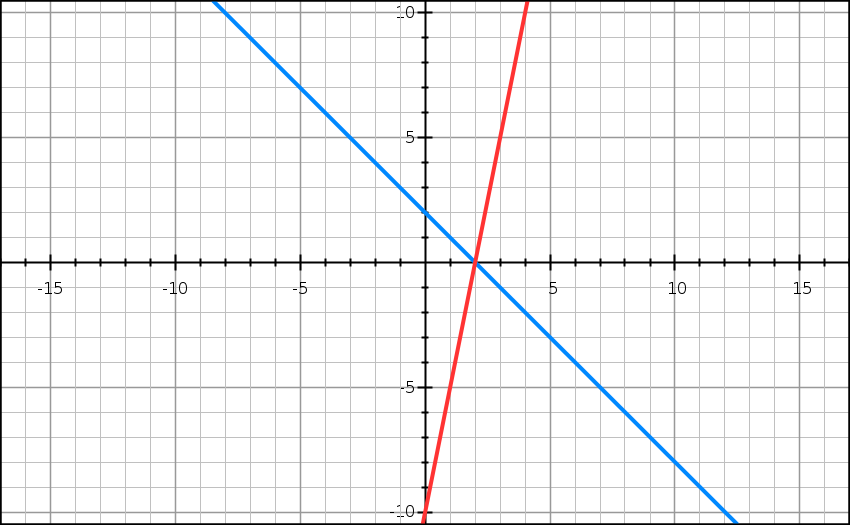Im Punkt x = 2, y = 0 schneiden sich die Geraden. Das LGS ist für diese Werte also gültig.
Nicht alle Geraden schneiden sich jedoch. Zwei Geraden können auch parallel oder identisch sein.
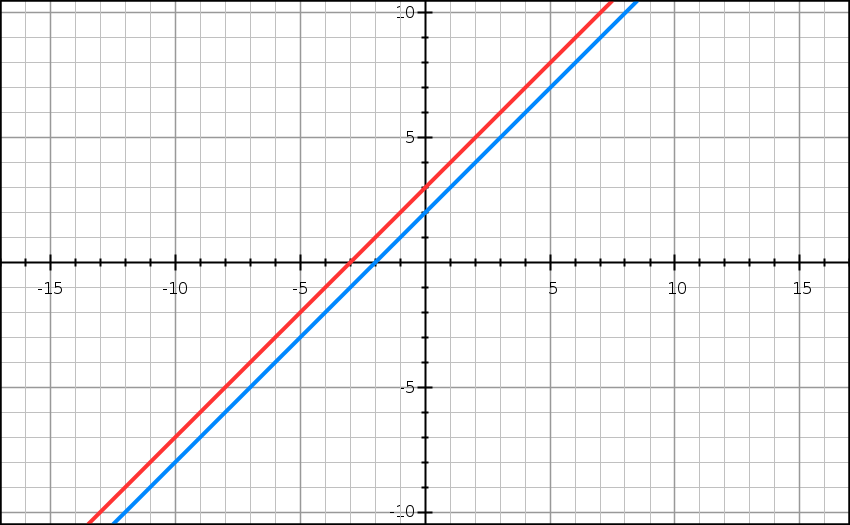
Sind die beiden Geraden parallel, so gibt es keinen Punkt, für den sie gleich sind. Das LGS hat also keine Lösung. Ein einfaches Beispiel für diesen Fall ist das folgende Gleichungssystem:
y = x + 2
y = x + 3
Im Koordinatensystem erkennst du sofort, dass diese beiden Geraden sich nie schneiden.
Zwei Gleichungen können auch identisch sein, obwohl sie eine unterschiedliche Form haben. Dies ist für das folgende LGS der Fall:
y = x – 1
2y = 2x – 2
Dieses Gleichungssystem ist für alle Kombinationen von x und y gültig, die eine der beiden Gleichungen lösen. Und natürlich kann man auch diese Gerade graphisch darstellen, auch wenn man nur eine Linie sieht – die andere liegt darunter.
Ein lineares Gleichungssystem lösen
Graphische Lösung
Eine mögliche Art, lineare Gleichungssysteme zu lösen, haben wir quasi schon vorgestellt: die graphische Lösung. Wenn du die Gleichungen des Gleichungssystems so umformst, dass du ihre Geraden zeichnen kannst, kannst du die Lösung des Gleichungssystems direkt aus dem Graphen ablesen.
Als Beispiel werden wir das folgende lineare Gleichungssystem lösen:
5y – 15x = 20
x = y – 2
Dieses Gleichungssystem lösen wir in drei Schritten.
Schritt 1: Gleichungen umformen
Als erstes musst du beide Gleichungen so umformen, dass auf der linken Seite nur y steht.
Gleichung 1:
5y – 15x = 20 | + 15x
⇔ 5y = 15x + 20 | : 5
⇔ y = 3x + 4
Gleichung 2:
x = y – 2 | – y
⇔ x – y = – 2 | – x
⇔ -y = -x – 2 | •(-1)
⇔ y = x + 2
Schritt 2: Geraden im Koordinatensystem einzeichnen
Im Koordinatensystem trägst du nun die beiden Gleichungen ab.
Schritt 3: Lösung ablesen
Nun musst du die Werte für den Schnittpunkt der beiden Geraden im Koordinatensystem ablesen. Er liegt bei (-1 | 1), die Lösung lautet also x = – 1, y = 1.
Additionsverfahren
Gleichungen mit einer Variablen kannst du bereits lösen. Das Additionsverfahren sorgt dafür, dass du zunächst eine Gleichung mit nur einer Variablen lösen musst. Hierzu eliminierst du eine Variable aus einer der beiden Gleichungen. Dies kannst du tun, indem du die beiden Gleichungen miteinander verrechnest.
Schauen wir uns das Beispiel an. Wenn du das 15-fache der zweiten Gleichung zur ersten Gleichung addierst, fällt dort das x weg. Du könntest genauso gut so rechnen, dass das y wegfällt. Wichtig ist, dass du ein n-faches der einen Gleichung zur anderen addierst oder von ihr abziehst und im Ergebnis nur noch eine Variable bleibt. Du kannst auch in mehreren Rechenschritten vorgehen.
Wir lösen wieder das LGS von oben:
5y – 15x = 20
x = y – 2
5y – 15x = 20 | + 15x
⇔ 5y – 15x + 15x = 20 + 15 y – 30
⇔ 5y = 20 + 15 y – 30
Nun hast du nur noch eine Variable, nach der du die Gleichung auflösen kannst.
⇔ 5y = 20 + 15 y – 30 | – 15y
⇔-10y = -10 | :-10
⇔ y = 1
Da du jetzt den Wert von y kennst, kannst du ihn in eine beliebige der beiden Gleichungen einsetzen und x einfach ausrechnen. Wir nehmen hierzu die zweite Gleichung, weil hier weniger Umformungen nötig sind.
x = 1 – 2 = -1
Wir kommen also mit dem Additionsverfahren – natürlich – auf dasselbe Ergebnis wie mit der graphischen Methode.
Einsetzungsverfahren
Beim Einsetzungsverfahren machst du dir zunutze, dass beide Gleichungen gleichzeitig gelten müssen. Wenn du nun eine der beiden Gleichungen so umformst, dass auf einer Seite nur eine Variable steht, kannst du die andere Seite in der anderen Gleichung an Stelle der Variable einsetzen – die Werte sind ja gleich.
In unserem Beispiel haben wir Glück und eine Gleichung hat schon genau die Form, die wir benötigen: x = y – 2. Wir setzen also in der anderen Gleichung statt x den Term y – 2 ein und lösen diese Gleichung dann nach y auf.
5y – 15x = 20
⇔ 5y – 15 • (y – 2) = 20
⇔ 5y – 15y + 30 = 20 | – 30
⇔ -10y = -10 | : -10
⇔ y = 1
Diesen Wert kannst du nun wieder in die Gleichung einsetzen (wie unter Additionsverfahren gezeigt) und erhältst auch hier dasselbe Ergebnis.
Gleichsetzungsverfahren
Beim Gleichsetzungsverfahren löst du beide Gleichungen nach derselben Variable auf und setzt die Ergebnisse miteinander gleich. Dann kannst du wieder nach der anderen Variablen auflösen und das Ergebnis in die andere Gleichung einsetzen.
Wir entscheiden uns hier dafür, nach y aufzulösen. Das haben wir bei der graphischen Lösung schon getan. Unser umgeformtes Gleichungssystem sieht also so aus:
y = 3x + 4
y = x + 2
Da y = y ist, können wir die anderen beiden Seiten ebenfalls gleichsetzen und erhalten:
3x + 4 = x + 2 | – x
⇔ 2x + 4 = 2 | – 4
⇔ 2x = -2 | : 2
⇔ x = -1
Dieses Ergebnis können wir nun in eine der beiden Gleichungen einsetzen. Wir nehmen die zweite.
-1 = y – 2 | +1
⇔ 0 = y – 1 | -y
⇔ -y = -1 | : (-1)
⇔ y = 1
Weitere Verfahren
Du kennst nun vier verschiedene Verfahren, um lineare Gleichungssysteme zu lösen. Alle vier sind gleich gut. Welches du einsetzt, hängt oft auch davon ab, in welcher Form die Gleichungen schon vorliegen – und natürlich von der Aufgabenstellung. Daher solltest du alle vier Verfahren gut kennen.
Wie du vielleicht festgestellt hast, haben wir nur lineare Gleichungssysteme mit zwei Gleichungen gelöst. Dies wird für dich während der Schulzeit wahrscheinlich ausreichen. Es gibt jedoch auch Methoden, mit denen du sehr leicht Gleichungssysteme mit mehr als zwei Variablen lösen kannst. Hierzu zählen der Gauß-Algorithmus, die Cramersche Regel und der Gauß-Jordan-Algorithmus. Diese lernst du jedoch normalerweise erst im Mathe-Studium kennen.
Lineare Gleichungssysteme lassen sich außerdem als Matrizen darstellen. Mehr zur Matrizenrechnung findest du in diesem Artikel.
Wie hilfreich war dieser Beitrag?
Klicke auf die Sterne um zu bewerten!