Potenzfunktionen und Wurzelfunktionen

Als Bausteine der Polynomfunktionen sind Potenzfunktionen in der Mathematik häufig zu finden. Sie beschreiben Zusammenhänge wie Kreisumfang und Radius, Kraft und Beschleunigung, Halbachse und Umlaufzeit von Planeten und vieles mehr.

Vorbemerkung

In diesem Text werden für die horizontale Achse x und für die vertikale Achse immer y = Funktionswert verwendet.

Potenzfunktionen

Mathematische Funktionen der Form

f_x = ax^r, dabei sind a,r ∈ R, nennt man Potenzfunktionen.

Für r = 1/n mit  n ∈ ℕ nennt man solche Funktionen Wurzelfunktionen, dazu weiter im Text mehr. Unterscheiden wir zunächst ein paar besondere Potenzfunktionen.

Sonderfälle

In der Abbildung siehst du einige Beispiele für Sonderfälle.

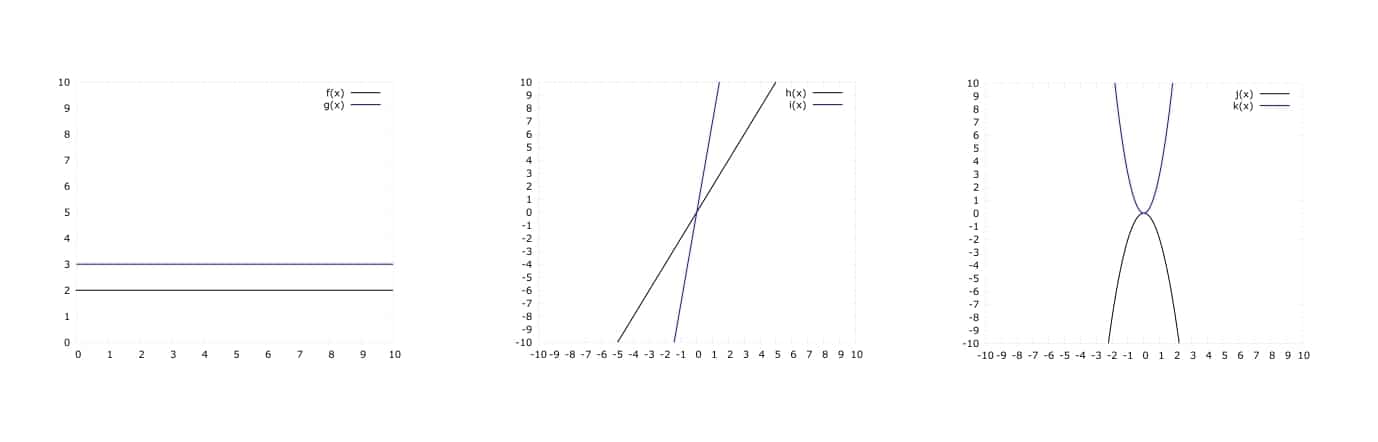Für r=0 ergibt sich eine konstante Funktion f_x=a.

Abgebildete Fälle: f_x=2 und g_x=3.

Für r=1 ergibt sich eine lineare Funktion f_x=ax.

Abgebildete Fälle: h_x=2x und i_x=7x-

Für r=2 ergibt sich eine quadratische Funktion  f_x=ax².

Abgebildete Fälle:  j_x= -2•x² und k_x=3x²

Eigenschaften

Gerade natürliche Exponenten

Am Graph einer Potenzfunktion lassen sich gut einige Eigenschaften erkennen.

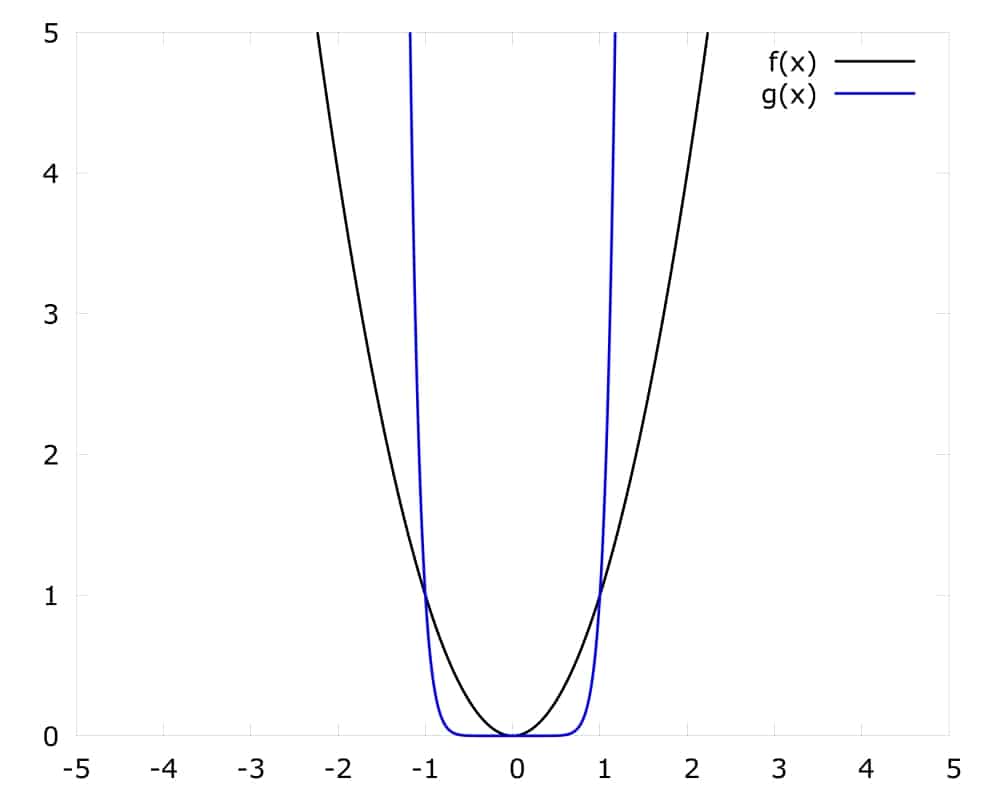
Hier siehst du die Graphen der Funktionen f_x= x² und g_x= x¹⁰.

Wie du gut erkennen kannst, verlaufen beide Funktionen durch die Punkte (1|1) und (-1|1). Warum? Eins hoch eine beliebige natürliche Zahl ergibt immer wieder 1. Die Funktion g_x= x¹⁰ steigt zunächst sehr viel langsamer an als f_x= x².

Woran liegt das?

Wenn du eine Zahl kleiner als 1, z.B. 0,8, mehrfach mit sich selbst multiplizierst, wird das Ergebnis immer kleiner 0,8²=0,8•0,8=0,64. Je größer der Exponent wird, desto stärker werden die Werte der Funktion für x<1 gedämpft und desto rapider steigen sie nach der Zahl 1. Da 1^x = 1, bleibt die 1 hier quasi neutral, während sich die Bereiche zwischen 0 und 1 und ab 1 unterschiedlich entwickeln.

Natürliche Exponenten

In der Abbildung siehst du die Funktionen f_x = x³ und f_x= x⁵

Gerade Exponenten ergeben Potenzfunktionen, welche auf beiden Seiten von x=0 positive Werte aufweisen, da eine negative Zahl mal eine negative Zahl eine positive Zahl ergibt. Ungerade Exponenten, wie hier 3 und 5 können jedoch für x < 0 Funktionswerte unter y=0 ergeben. Der Graph scheint links von x=0 auf die andere Seite der Gerade y=0 gespiegelt zu sein.

Für Potenzfunktionen mit natürlichen Exponenten gilt als Definitionsmenge R, es gibt keinen Punkt auf der x-Achse, für den es keinen Funktionswert gibt.

Negative Exponenten

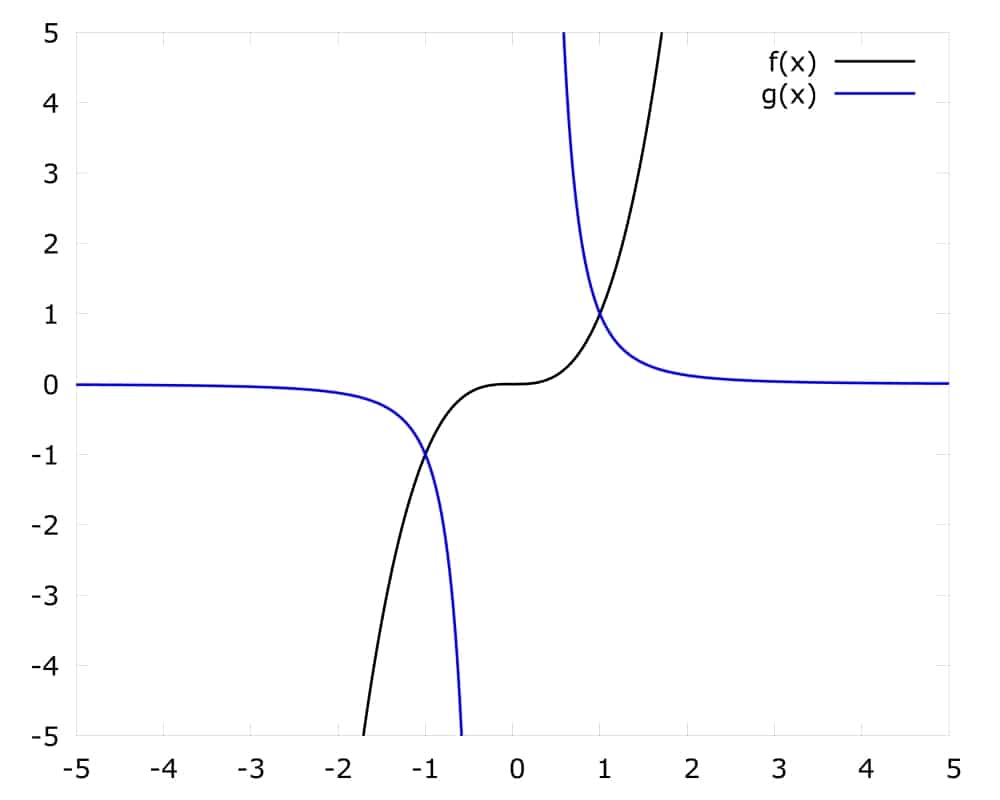
Für r < 0, r ∈ ℤ, ergeben sich Funktionen wie g_x=x^-3. Zum Vergleich ist auch f_x=x³ eingezeichnet.

Wie du an der Abbildung sehen kannst, führt der negative Exponent dazu, dass die Funktion den Kehrwert der Funktion mit gleich großem positiven Exponenten annimmt.

Dass das so sein muss, ergibt sich aus dem Potenzgesetz

Denn

Hinweis: Für Funktionen g_x=3•x^-3 und f_x=3*x³$ wäre der Kehrwert der Funktion nicht mehr gleich dem Wert der anderen Funktion, da ein Koeffizient a ungleich 1 vor dem x steht.

Für solche Funktionen ergibt sich als Definitionsmenge die Menge der reellen Zahlen ohne 0. Da Teilen durch die Zahl 0 nicht definiert ist, ergibt sich hier die Einschränkung.

Symmetrie

Dir wird aufgefallen sein, dass einige der Graphen symmetrisch zur y-Achse (x=0) sind, während andere punktsymmetrisch zum Ursprung (0|0) sind.

Funktionen, welche einen zur y-Achse symmetrischen Graphen haben, nennt man gerade Funktionen.

Es gilt: f_-x = f_x

Hinweis: Gerade Funktion heißt nicht, dass der Graph eine Gerade ist.

Funktionen, deren Graphen punktsymmetrisch zum Koordinatenursprung sind, nennt man ungerade.

Es gilt: f_-x = -f_x

Potenzfunktionen, deren r eine ganze Zahl ist, sind symmetrisch. Eine gerade Potenzfunktion hat ein geradzahliges r und eine ungerade Potenzfunktion ein ungerades r.

Potenzfunktionen mit rationalen Exponenten

Lässt man für r in f_x=ax^r alle rationalen Zahlen zu, so können sich weitere Varianten ergeben.

Hier siehst du die Funktionen f_x=x^0,5 und g_x=x^3,5.

Die beiden Funktionen lassen sich auch schreiben als:

f_x=x^0,5 = √x  und

mit dem Potenzgesetz x^r•x^s=x^r+s ergibt sich für r = 3,5

g_x=x^3,5 = √x • x³

Wie du sehen kannst, handelt es sich um Wurzelfunktionen.

Warum ergeben Brüche im Exponenten Wurzeln?

Die Grundlage dafür liegt wieder einmal in den Potenzgesetzen.

x^r • x^s = x^r+s

Eine Funktion f_x=x^(1/2) entspricht also der Frage, welches x^0,5 • x^0,5 = x¹ entspricht.

Bei der Multiplikation addieren sich die Exponenten, man kann also einen Wert für x^0,5 suchen, der mit sich selbst multipliziert x ergibt.

Beispiel: Die Quadratwurzel von 100 √100 = 100^(1/2) entspricht der Zahl, welche mit sich selbst multipliziert 100 ergibt, diese Zahl ist 10.

Kubikwurzel

So wie x^0,5 als √x definiert ist, kannst du auch die Begründung für die Kubikwurzel von x x^(1/3) verstehen. Welcher Wert von x^(1/3) ergibt x, wenn man ihn dreimal mit sich selbst multipliziert? Warum dreimal? Weil drei Mal ein Drittel wieder 1 ergeben x^(1/3) • x^(1/3) •x^(1/3) = x.

Frage in der Schule nach, ob du bei ungeraden Wurzeln auch negative x verwenden kannst, denn nicht im ganzen Land wird das einheitlich gemacht.

Analytische Eigenschaften

Stetigkeit

Bezüglich der Definitionsmenge sind alle Potenzfunktionen stetig. Überlege dir also genau, welche Werte für die unabhängige Variable erlaubt sind. Einige Beispiele für Definitionsmengen findest du oben.

Ableitung

Für eine Potenzfunktion f_x=ax^r ergibt sich die Ableitung f’_x = arx^{{ r-1)}  .

Mit dieser Formel kannst du alle Potenzfunktionen mit einem x ≠ 0 $ ableiten. Für r ≥ 1 ist sie auch für x=0 richtig.

Beispiel: Gesucht ist die Ableitung von f_x=3x³  .

Die Ableitung lautet also f’_x = 3•3x^3-1  vereinfacht f’_x = 9x² .

Integration

Für eine rationale Zahl r ≠ -1 gilt das Integrationsmuster Bitte beachte dabei, dass das Intervall, über das integriert wird, eine Teilmenge der Definitionsmenge ist.

Beispiel:

Für den Sonderfall r=-1 gilt: