Das Urnenmodell ist ein besonders weit verbreitetes Modell in der Wahrscheinlichkeitsrechnung. Wir stellen dir hier die beiden Varianten des Modells vor und erklären dir, was du bei der Berechnung von Wahrscheinlichkeiten beachten musst.
Was ist eine Wahrscheinlichkeit und wie berechnest du sie?
Die Wahrscheinlichkeit für ein Ereignis sagt aus, wie sicher oder unsicher es ist, dass dieses Ereignis im Vergleich zu anderen möglichen Ereignissen eintritt.
[quads id=1]Da wir nicht wissen, was in der Zukunft passiert, ist es gut, sich Gedanken über Wahrscheinlichkeiten zu machen. Wir machen dies im Alltag oft. Im Sommer ist die Wahrscheinlichkeit für gutes Wetter hoch, also nehmen wir keinen Schirm mit. Das heißt aber nicht, dass es nie im Sommer regnet, nur eben seltener.
In der Mathematik ermittelt man die Wahrscheinlichkeit für das Eintreten eines bestimmten Ereignisses, indem man die Anzahl der gesuchten Ergebnisse durch die Anzahl der möglichen Ergebnisse teilt.
Das ist einfacher am Beispiel zu verstehen. Wenn du mit einem normalen Würfel würfelst, hast du 6 mögliche Ergebnisse. Da es keinen Grund gibt, anzunehmen, dass eine Zahl häufiger fällt als die anderen, ist die Wahrscheinlichkeit für jedes einzelne Ergebnis 1/6.
Wenn du nun wissen möchtest, wie hoch die Wahrscheinlichkeit ist, eine gerade Zahl zu würfeln, rechnest du die Anzahl der gesuchten Ergebnisse (die 2, 4, und 6 sind gerade, also 3) durch die Anzahl der möglichen Ergebnisse (6). Die Wahrscheinlichkeit für eine gerade Zahl beträgt also 3/6. Dies kannst du zu ½ kürzen oder auch als 50% darstellen – alle Werte sagen dasselbe aus.
Das Urnenmodell
Als Urnenmodell bezeichnet man ein theoretisches Konstrukt, bei dem auseinem Behältnis – der Urne – gleich große Kugeln gezogen werden, die sich nur durch ihre Farbe oder durch eine aufgedruckte Zahl unterscheiden. Du kannst dir das wie bei der Ziehung der Lottozahlen vorstellen. Meist sollst du dann berechnen, wie hoch die Wahrscheinlichkeit ist, eine Kugel einer bestimmten Farbe zu ziehen.
Mehrfaches Ziehen mit und ohne Zurücklegen
Meistens will man Wahrscheinlichkeiten nicht nur für ein Ereignis wissen, sondern für mehrere Ereignisse, die hintereinander eintreten. Wenn du beispielsweise ein Spiel spielst, bei dem es wichtig ist, Sechsen zu würfeln, willst du vielleicht wissen, wie wahrscheinlich es ist, zwei Sechsen hintereinander zu würfeln.
Zur Visualisierung sind hier Entscheidungsbäume hilfreich. Sie zeigen nämlich, wie viele Möglichkeiten es gibt, sobald du mehrere Würfe oder Ziehungen hintereinander durchführst.
Dabei unterscheidet man danach, ob man beim zweiten Versuch dieselben Ausgangsbedingungen hat wie beim ersten oder ob der erste die Bedingungen für den zweiten ändert.
[quads id=2]Wenn du einen Würfel 100 Mal wirfst, hast du bei jedem Wurf wieder dieselben Wahrscheinlichkeiten, der Würfel hat nämlich immer sechs Seiten. Dasselbe Ergebnis erhältst du, wenn du aus einer Urne Kugeln ziehst und sie nach dem Ziehen wieder zurücklegst.
Legst du die Kugeln jedoch nicht zurück, ändern sich die Wahrscheinlichkeiten. Hast du Kugeln, die von 1 bis 5 beschriftet sind, ist die Wahrscheinlichkeit für jede Kugel im ersten Zug 1/5. Wenn du im ersten Zug eine 2 ziehst und nicht zurücklegst, kannst du sie im zweiten Zug nicht mehr ziehen. Die Wahrscheinlichkeit für eine 2 im zweiten Zug ist dann 0. Die Wahrscheinlichkeit für die anderen Kugeln erhöht sich jedoch, denn es sind ja nur noch vier verschiedene Kugeln in der Urne. Für jede beträgt dann die Wahrscheinlichkeit ¼. Beides betrachten wir im Folgenden.
Ziehen mit Zurücklegen
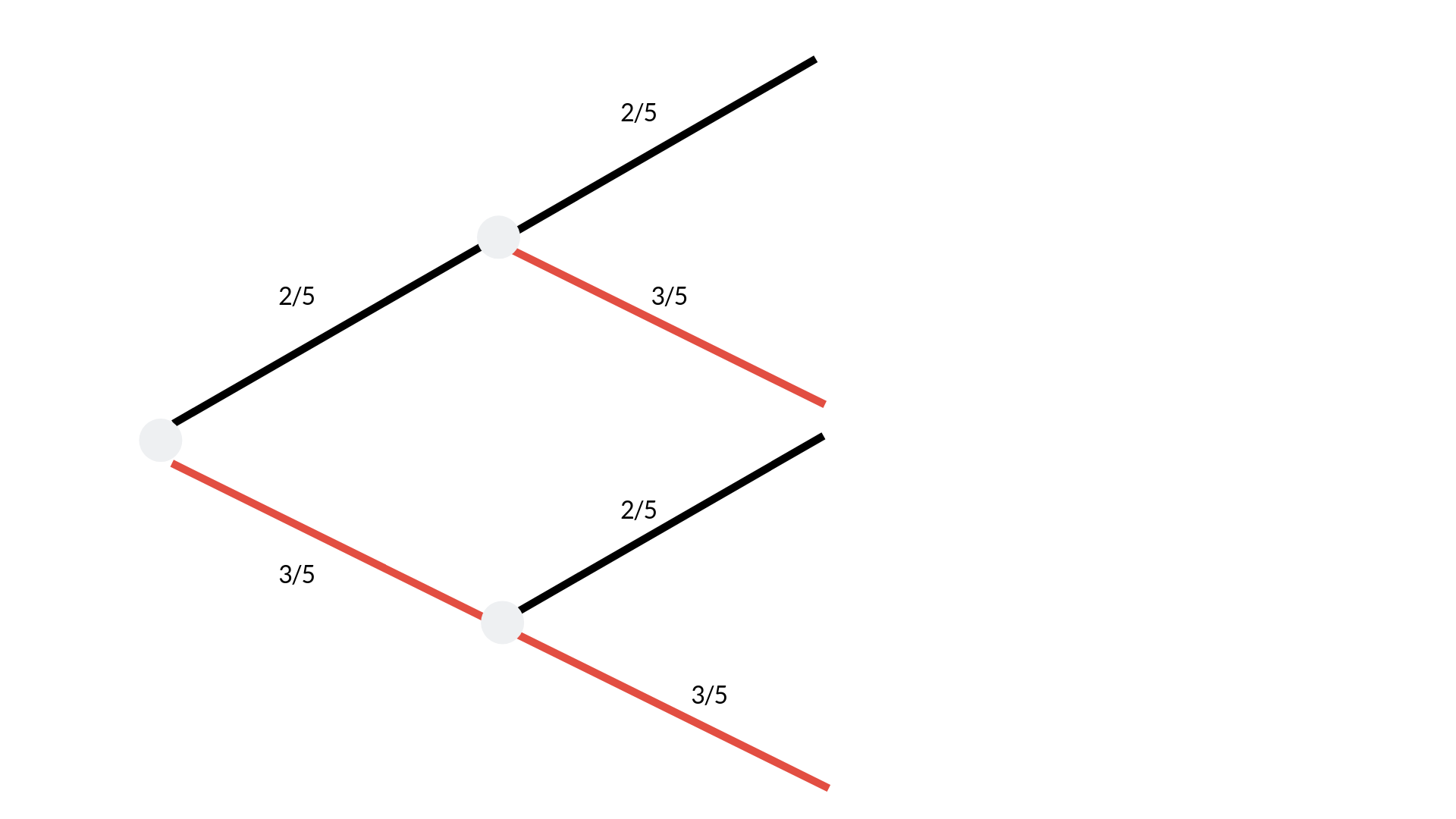
Wenn du eine Urne mit 40 roten und 60 weißen Kugeln hast und zwei Mal mit Zurücklegen ziehst, ergeben sich für beide Züge dieselben Wahrscheinlichkeiten: 40/100 bzw. 2/5 für rote Kugeln und 60/100 bzw. 3/5 für weiße Kugeln. Im Baumdiagramm sieht das wie folgt aus:
Wenn du nun wissen möchtest, wie hoch die Wahrscheinlichkeit ist, dass du in der ersten Ziehung eine rote und in der zweiten eine weiße ziehst, musst du das Baumdiagramm entsprechend abgehen und die Wahrscheinlichkeiten auf den Ästen multiplizieren.
[quads id=3]Ziehen ohne Zurücklegen
Wenn du aus einer Urne Kugeln ziehst und diese nicht zurücklegst, ist die Wahrscheinlichkeit für die verbleibenden Kugeln im zweiten Zug eine andere. Wenn du eine Urne mit nur vier Kugeln hast, von denen zwei weiß und zwei rot sind, beträgt die Wahrscheinlichkeit für jede Farbe in jedem Zug 2/4 oder ½. Im zweiten Zug ändert sie sich aber in Abhängigkeit von der ersten gezogenen Farbe. Wenn du im ersten Zug eine weiße Kugel gezogen hast, ist nur noch eine weiße in der Urne, und insgesamt sind es nur noch drei Kugeln. Die Wahrscheinlichkeit, die weiße Kugel zu ziehen, beträgt also nur noch 1/3. Da noch zwei rote Kugeln vorhanden sind, beträgt die Wahrscheinlichkeit, eine von diesen zu ziehen, 2/3. Ziehst du im ersten Zug eine rote Kugel, sehen die Wahrscheinlichkeiten im zweiten Zug umgekehrt aus.
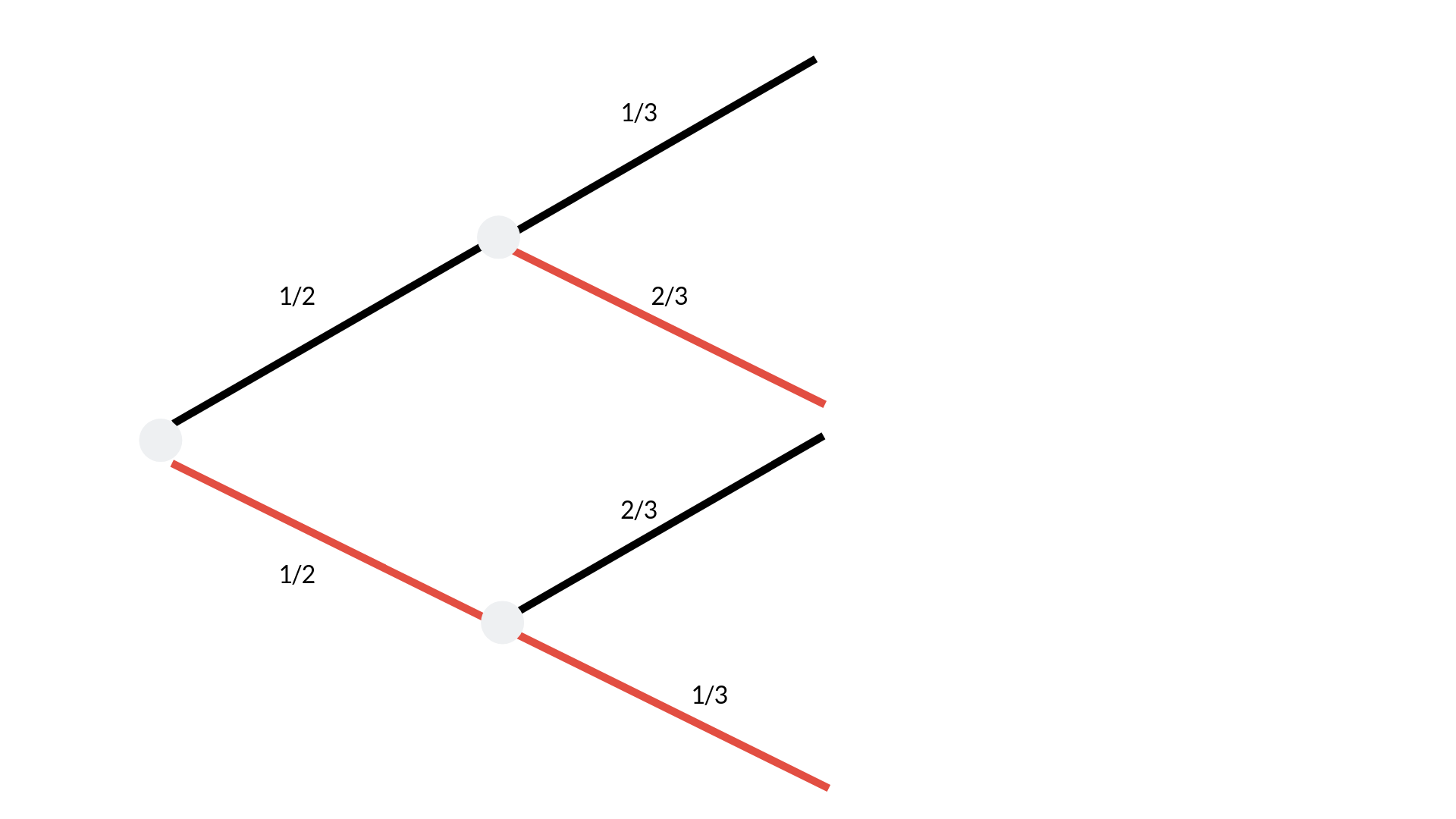
Im Baumdiagramm sieht das dann so aus:
Sollst du ausrechnen, wie hoch die Wahrscheinlichkeit ist, im ersten Zug eine rote und im zweiten Zug eine weiße Kugel zu ziehen, gehst du wieder den Pfad im Baumdiagramm nach und multiplizierst die entsprechenden Wahrscheinlichkeiten miteinander, also 1/2 • 2/3 = 2/6 = 1/3.
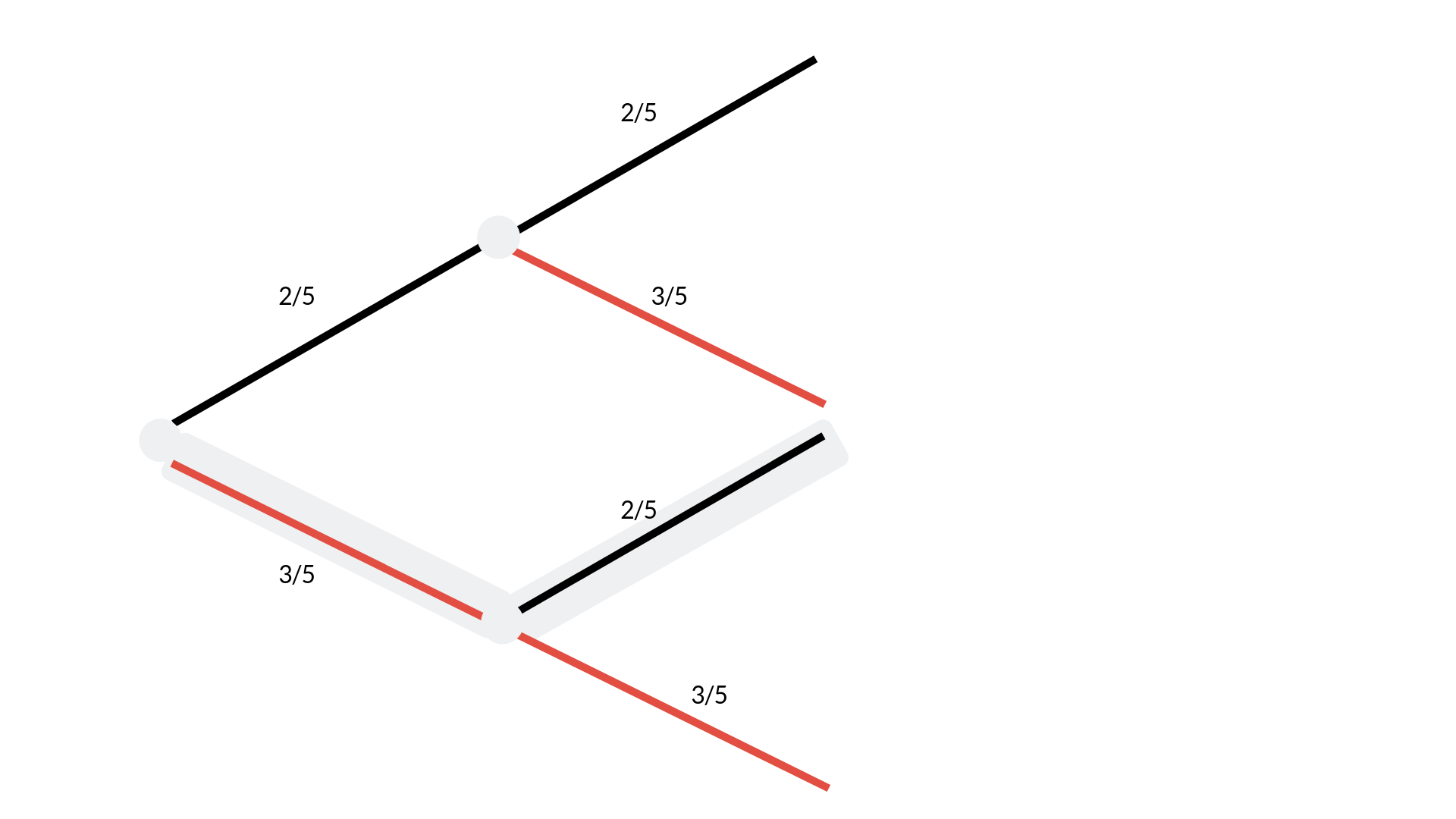
Du gehst also zuerst den roten Pfad entlang und von dort den schwarzen und multiplizierst 3/5 • 2/5. Als Gesamtwahrscheinlichkeit erhältst du dann 6/25.