Vektoren sind ein wichtiger Bestandteil der linearen Algebra. Wir erklären dir in diesem Artikel, was Vektoren sind und wie du mit ihnen rechnest.
Was sind Vektoren?
Vektoren sind Richtungsangaben im Koordinatensystem. Wenn du dich von einem Punkt A zu einem anderen Punkt B bewegen möchtest, kannst du angeben, wie viele Einheiten du dich auf der x-Achse nach rechts bewegen musst und wie viele auf der y-Achse nach oben. In der Graphik kommst du von Punkt A nach Punkt B, indem du dich zwei Einheiten nach rechts auf der x-Achse bewegst und einen nach oben auf der y-Achse.
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=1]
[su_divider top=“no“ divider_color=“#eeeeee“]
Diese Richtungsangabe kannst du als Vektor in der Form
schreiben. g1 bezeichnet man dann als Richtungsvektor, denn er gibt an, wie du von einem beliebigen Punkt A im zweidimensionalen Raum zu einem entsprechenden Punkt B gelangen kann. Der obere Wert gibt die Bewegung auf der x-Achse an, der untere die Bewegung auf der y-Achse.
Vektoren gibt es jedoch nicht nur im zwei-, sondern auch im drei- oder mehrdimensionalen Raum. Im dreidimensionalen Raum bewegt sich die Richtungsangabe dann nicht in der Ebene, sondern hat auch noch eine Höhe. Ein Vektor im dreidimensionalen Raum hat also auch immer einen Wert für die z-Achse. Das Zeichnen wird dann natürlich ein wenig schwieriger, aber den Vektor
kann man zum Beispiel so darstellen:
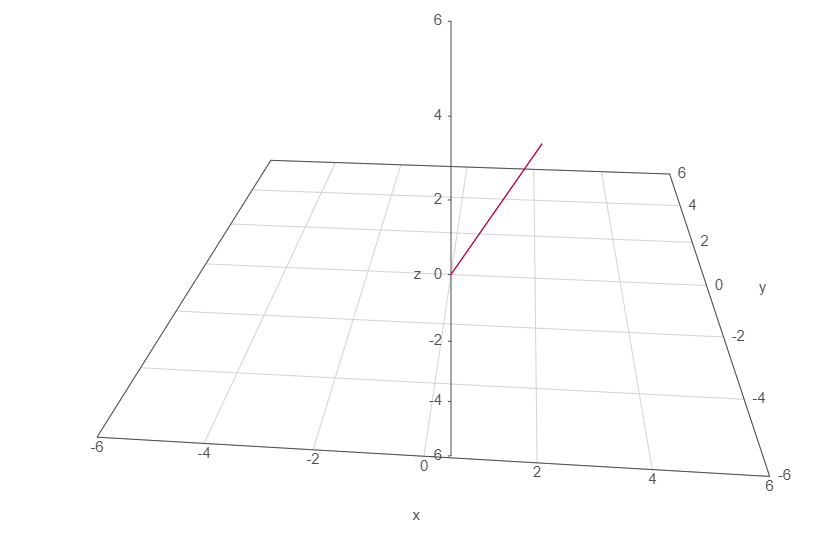Wenn du einen Vektor am Nullpunkt des Koordinatensystems beginnen lässt, wird er übrigens zum Ortsvektor, denn du gibst mit ihm gleichzeitig die Lage des Endpunkts an.
Vektorrechnung
Mit Vektoren kann man verschiedene Rechenoperationen durchführen. Dafür ist es wichtig, dass die Vektoren dieselbe Dimension haben. Wir rechnen im Folgenden mit Vektoren in der Ebene, also im zweidimensionalen Raum. Für alle anderen Vektoren gelten die Regeln jedoch genauso.
Vektoren addieren
Zwei Vektoren kannst du ganz einfach addieren, indem du die Werte der verschiedenen Vektoren Reihe für Reihe addierst, also
Das kannst du auch ganz leicht im Koordinatensystem nachvollziehen. Wenn du von einem Punkt zuerst a und dann b gehst, kommst du an dem Punkt an, der durch den Vektor beschrieben wird, der die Summe der beiden bildet. Graphisch sieht das wie folgt aus:
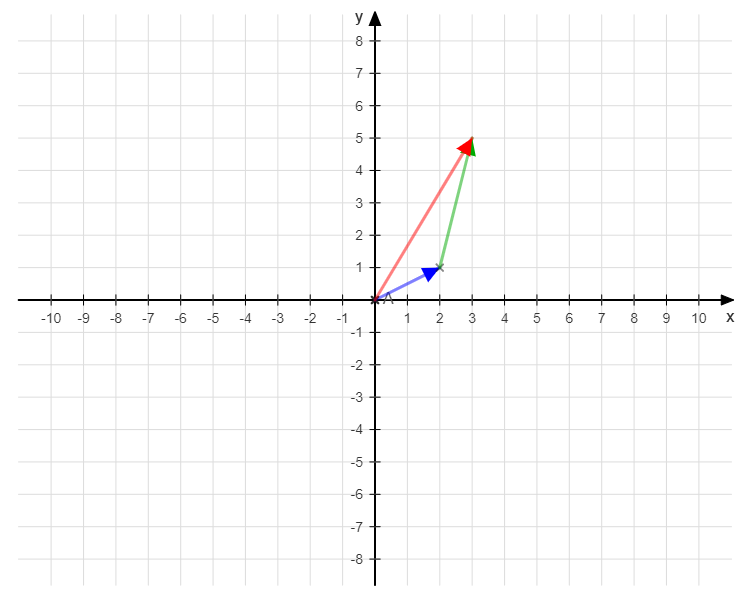Die Rechnung für die Graphik lautet:
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=2]
[su_divider top=“no“ divider_color=“#eeeeee“]
Vektoren subtrahieren
Die Subtraktion von Vektoren funktioniert nach demselben Muster, du subtrahierst einfach zeilenweise die einzelnen Werte voneinander.
Im Beispiel (die Umkehrrechnung zu oben) sieht das dann wie folgt aus:
[su_divider top=“no“ divider_color=“#eeeeee“]
[quads id=3]
[su_divider top=“no“ divider_color=“#eeeeee“]
Das Skalarprodukt berechnen
Eine weitere wichtige Möglichkeit zur Vektorrechnung ist das Skalarprodukt. Hier erhältst du als Ergebnis eine Zahl. Du multiplizierst die Werte reihenweise und addierst die Ergebnisse dann miteinander.
